Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138656 by ajfour last updated on 16/Apr/21

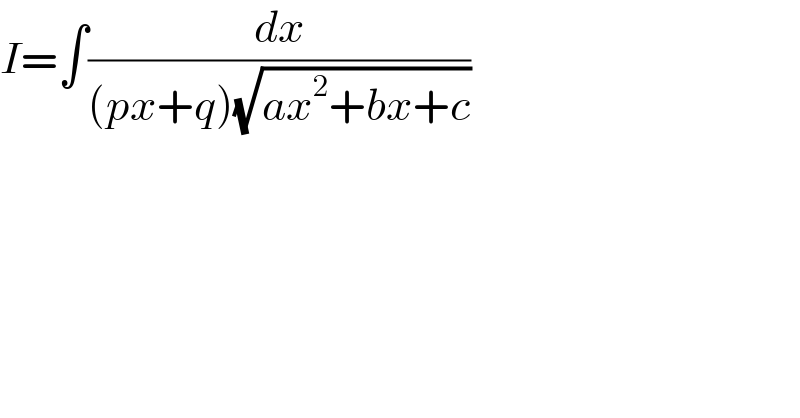
I=∫(dx/((px+q)(√(ax^2 +bx+c))))

$${I}=\int\frac{{dx}}{\left({px}+{q}\right)\sqrt{{ax}^{\mathrm{2}} +{bx}+{c}}} \\ $$

Answered by Ar Brandon last updated on 16/Apr/21

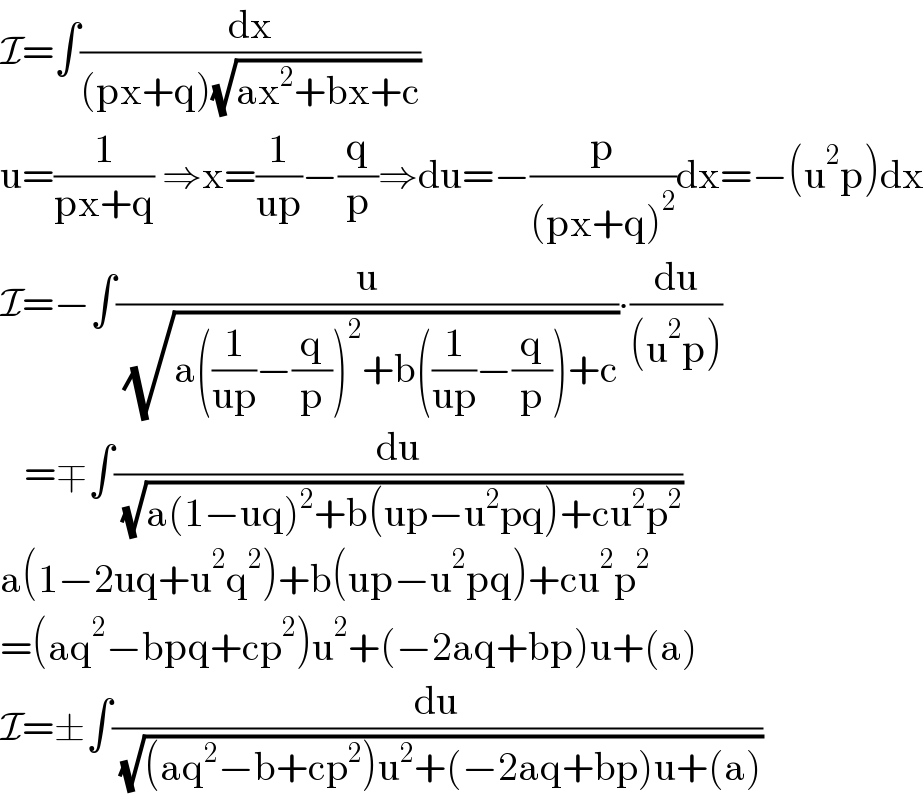
I=∫(dx/((px+q)(√(ax^2 +bx+c)))) u=(1/(px+q)) ⇒x=(1/(up))−(q/p)⇒du=−(p/((px+q)^2 ))dx=−(u^2 p)dx I=−∫(u/( (√(a((1/(up))−(q/p))^2 +b((1/(up))−(q/p))+c))))∙(du/((u^2 p))) =∓∫(du/( (√(a(1−uq)^2 +b(up−u^2 pq)+cu^2 p^2 )))) a(1−2uq+u^2 q^2 )+b(up−u^2 pq)+cu^2 p^2 =(aq^2 −bpq+cp^2 )u^2 +(−2aq+bp)u+(a) I=±∫(du/( (√((aq^2 −b+cp^2 )u^2 +(−2aq+bp)u+(a)))))

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{px}+\mathrm{q}\right)\sqrt{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}} \\ $$$$\mathrm{u}=\frac{\mathrm{1}}{\mathrm{px}+\mathrm{q}}\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{up}}−\frac{\mathrm{q}}{\mathrm{p}}\Rightarrow\mathrm{du}=−\frac{\mathrm{p}}{\left(\mathrm{px}+\mathrm{q}\right)^{\mathrm{2}} }\mathrm{dx}=−\left(\mathrm{u}^{\mathrm{2}} \mathrm{p}\right)\mathrm{dx} \\ $$$$\mathcal{I}=−\int\frac{\mathrm{u}}{\:\sqrt{\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{up}}−\frac{\mathrm{q}}{\mathrm{p}}\right)^{\mathrm{2}} +\mathrm{b}\left(\frac{\mathrm{1}}{\mathrm{up}}−\frac{\mathrm{q}}{\mathrm{p}}\right)+\mathrm{c}}}\centerdot\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} \mathrm{p}\right)} \\ $$$$\:\:\:=\mp\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{a}\left(\mathrm{1}−\mathrm{uq}\right)^{\mathrm{2}} +\mathrm{b}\left(\mathrm{up}−\mathrm{u}^{\mathrm{2}} \mathrm{pq}\right)+\mathrm{cu}^{\mathrm{2}} \mathrm{p}^{\mathrm{2}} }} \\ $$$$\mathrm{a}\left(\mathrm{1}−\mathrm{2uq}+\mathrm{u}^{\mathrm{2}} \mathrm{q}^{\mathrm{2}} \right)+\mathrm{b}\left(\mathrm{up}−\mathrm{u}^{\mathrm{2}} \mathrm{pq}\right)+\mathrm{cu}^{\mathrm{2}} \mathrm{p}^{\mathrm{2}} \\ $$$$=\left(\mathrm{aq}^{\mathrm{2}} −\mathrm{bpq}+\mathrm{cp}^{\mathrm{2}} \right)\mathrm{u}^{\mathrm{2}} +\left(−\mathrm{2aq}+\mathrm{bp}\right)\mathrm{u}+\left(\mathrm{a}\right) \\ $$$$\mathcal{I}=\pm\int\frac{\mathrm{du}}{\:\sqrt{\left(\mathrm{aq}^{\mathrm{2}} −\mathrm{b}+\mathrm{cp}^{\mathrm{2}} \right)\mathrm{u}^{\mathrm{2}} +\left(−\mathrm{2aq}+\mathrm{bp}\right)\mathrm{u}+\left(\mathrm{a}\right)}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com