
Previous in Differential Equation Next in Differential Equation
Question Number 212307 by MrGaster last updated on 09/Oct/24
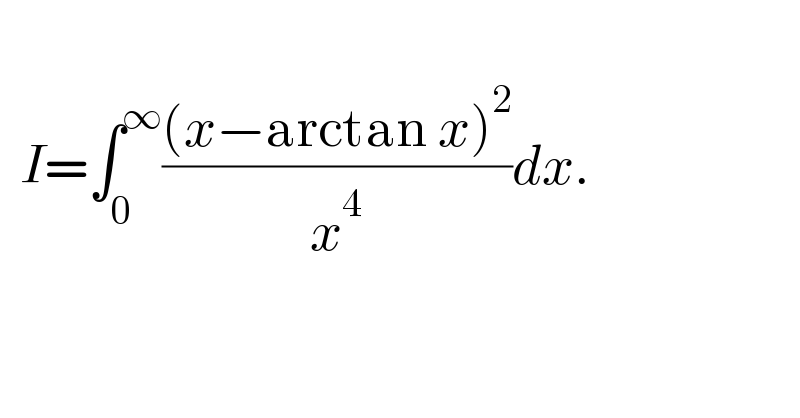
$$ \\ $$$$\:\:{I}=\int_{\mathrm{0}} ^{\infty} \frac{\left({x}−\mathrm{arctan}\:{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} }{dx}. \\ $$
Answered by Ghisom last updated on 09/Oct/24
![∫ (((x−arctan x)^2 )/x^4 )dx=A+B+C A=∫ (dx/x^2 )=−(1/x) B=−2∫ ((arctan x)/x^3 )dx= [by parts] =(1/x)+((x^2 +1)/x^2 )arctan x A+B=((x^2 +1)/x^2 )arctan x C=∫ ((arctan^2 x)/x^4 )dx= [t=arctan x] =∫ ((t^2 cos^2 t)/(sin^4 t))dt= [by parts] =D+E D=−(t^2 /(3tan^3 t))=−((arctan^2 x)/(3x^3 )) E=(2/3)∫(t/(tan^3 t))dt= [by parts] =F+G F=−(t/(3tan^2 t))−((2t)/3)ln sin t F=((arctan x)/3)(ln (x^2 +1) −2ln ∣x∣ −(1/x^2 )) G=H+J H=(1/3)∫(dt/(tan^2 t))=−(1/3)(t+(1/(tan t))) H=−(1/3)((1/x)+arctan x) all above x∈[0, ∞) J=(2/3)∫_0 ^(π/2) ln sin t dt=−((πln 2)/3) [this is easy ;−)] I get I=(π/3)(1−ln 2)](Q212315.png)
$$\int\:\frac{\left({x}−\mathrm{arctan}\:{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} }{dx}={A}+{B}+{C} \\ $$$${A}=\int\:\frac{{dx}}{{x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{{x}} \\ $$$${B}=−\mathrm{2}\int\:\frac{\mathrm{arctan}\:{x}}{{x}^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{1}}{{x}}+\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{arctan}\:{x} \\ $$$${A}+{B}=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{arctan}\:{x} \\ $$$${C}=\int\:\frac{\mathrm{arctan}^{\mathrm{2}} \:{x}}{{x}^{\mathrm{4}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arctan}\:{x}\right] \\ $$$$=\int\:\frac{{t}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:{t}}{\mathrm{sin}^{\mathrm{4}} \:{t}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$={D}+{E} \\ $$$${D}=−\frac{{t}^{\mathrm{2}} }{\mathrm{3tan}^{\mathrm{3}} \:{t}}=−\frac{\mathrm{arctan}^{\mathrm{2}} \:{x}}{\mathrm{3}{x}^{\mathrm{3}} } \\ $$$${E}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{t}}{\mathrm{tan}^{\mathrm{3}} \:{t}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$={F}+{G} \\ $$$${F}=−\frac{{t}}{\mathrm{3tan}^{\mathrm{2}} \:{t}}−\frac{\mathrm{2}{t}}{\mathrm{3}}\mathrm{ln}\:\mathrm{sin}\:{t} \\ $$$${F}=\frac{\mathrm{arctan}\:{x}}{\mathrm{3}}\left(\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:−\mathrm{2ln}\:\mid{x}\mid\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$${G}={H}+{J} \\ $$$${H}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{\mathrm{tan}^{\mathrm{2}} \:{t}}=−\frac{\mathrm{1}}{\mathrm{3}}\left({t}+\frac{\mathrm{1}}{\mathrm{tan}\:{t}}\right) \\ $$$${H}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{x}}+\mathrm{arctan}\:{x}\right) \\ $$$$\mathrm{all}\:\mathrm{above}\:{x}\in\left[\mathrm{0},\:\infty\right) \\ $$$${J}=\frac{\mathrm{2}}{\mathrm{3}}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{ln}\:\mathrm{sin}\:{t}\:{dt}=−\frac{\pi\mathrm{ln}\:\mathrm{2}}{\mathrm{3}} \\ $$$$\left.\:\:\:\:\:\left[\mathrm{this}\:\mathrm{is}\:\mathrm{easy}\:;−\right)\right] \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$${I}=\frac{\pi}{\mathrm{3}}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right) \\ $$
