
Question Number 210933 by mnjuly1970 last updated on 22/Aug/24
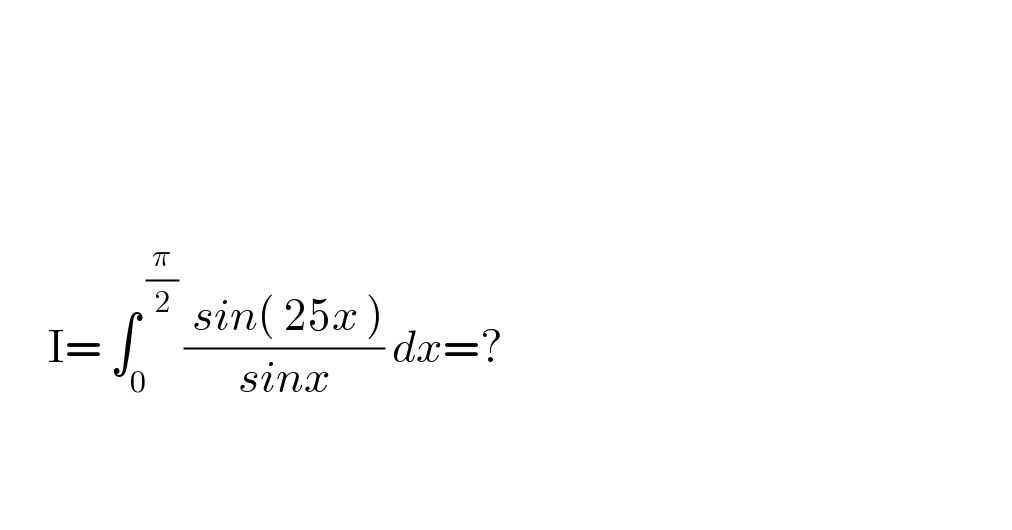
$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}\:} \frac{\:{sin}\left(\:\mathrm{25}{x}\:\right)}{{sinx}}\:{dx}=? \\ $$$$ \\ $$$$ \\ $$
Answered by Ghisom last updated on 22/Aug/24
![((sin 25x)/(sin x))=(((e^(25ix) −e^(−25ix) )/(2i))/((e^(ix) −e^(−ix) )/(2i)))= =1+Σ_(n=1) ^(12) (e^(2nxi) +e^(−2nxi) ) = =1+2Σ_(n=1) ^(12) cos 2nx ⇒ ∫_0 ^(π/2) ((sin 25x)/(sin x))dx=[x+Σ_(n=1) ^(12) ((sin 2nx)/n)]_0 ^(π/2) = =(π/2)](Q210941.png)
$$\frac{\mathrm{sin}\:\mathrm{25}{x}}{\mathrm{sin}\:{x}}=\frac{\frac{\mathrm{e}^{\mathrm{25i}{x}} −\mathrm{e}^{−\mathrm{25i}{x}} }{\mathrm{2i}}}{\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2i}}}= \\ $$$$=\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\left(\mathrm{e}^{\mathrm{2}{nx}\mathrm{i}} +\mathrm{e}^{−\mathrm{2}{nx}\mathrm{i}} \right)\:= \\ $$$$=\mathrm{1}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\:\mathrm{cos}\:\mathrm{2}{nx} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{25}{x}}{\mathrm{sin}\:{x}}{dx}=\left[{x}+\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\:\frac{\mathrm{sin}\:\mathrm{2}{nx}}{{n}}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} = \\ $$$$=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 23/Aug/24
$${thanks}\:{alot}\:{sir}\:.{excellent} \\ $$
