
Question Number 209624 by mnjuly1970 last updated on 16/Jul/24
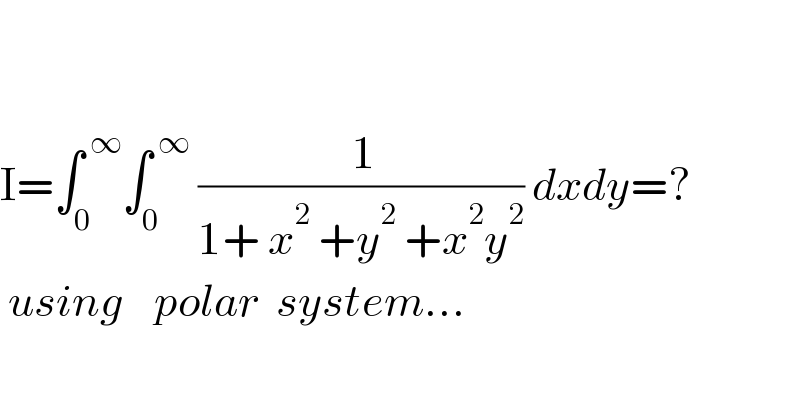
$$ \\ $$$$ \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \:\frac{\:\mathrm{1}}{\mathrm{1}+\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} {y}^{\mathrm{2}} }\:{dxdy}=? \\ $$$$\:{using}\:\:\:\:{polar}\:\:{system}... \\ $$
Answered by mr W last updated on 16/Jul/24
![=∫_0 ^∞ ∫_0 ^∞ (1/((1+x^2 )(1+y^2 )))dxdy =[∫_0 ^∞ (1/(1+x^2 ))dx]^2 =([tan^(−1) x]_0 ^∞ )^2 =((π/2))^2 =(π^2 /4)](Q209627.png)
$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}{dxdy} \\ $$$$=\left[\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right]^{\mathrm{2}} \\ $$$$=\left(\left[\mathrm{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\infty} \right)^{\mathrm{2}} \\ $$$$=\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
