
Question Number 6405 by FilupSmith last updated on 26/Jun/16
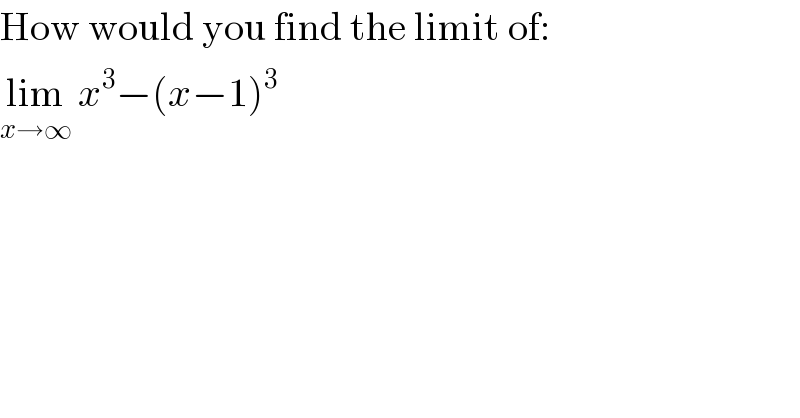
$$\mathrm{How}\:\mathrm{would}\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{of}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$
Commented by FilupSmith last updated on 26/Jun/16

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{expand}\:\mathrm{and}\:\mathrm{simplify}? \\ $$$$\mathrm{Or}\:\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{simpler}\:\mathrm{method}? \\ $$
Commented by Rasheed Soomro last updated on 27/Jun/16
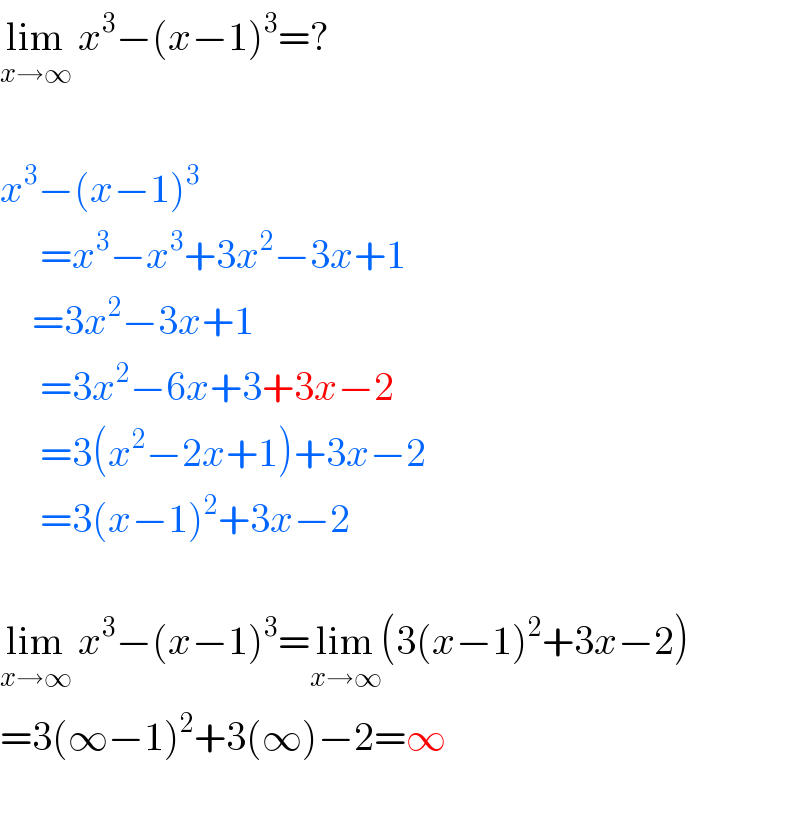
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} =? \\ $$$$ \\ $$$${x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:={x}^{\mathrm{3}} −{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1} \\ $$$$\:\:\:\:=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1} \\ $$$$\:\:\:\:\:=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{3}+\mathrm{3}{x}−\mathrm{2} \\ $$$$\:\:\:\:\:=\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{3}{x}−\mathrm{2} \\ $$$$\:\:\:\:\:=\mathrm{3}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{3}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\right)\:\:\: \\ $$$$=\mathrm{3}\left(\infty−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\left(\infty\right)−\mathrm{2}=\infty \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 27/Jun/16
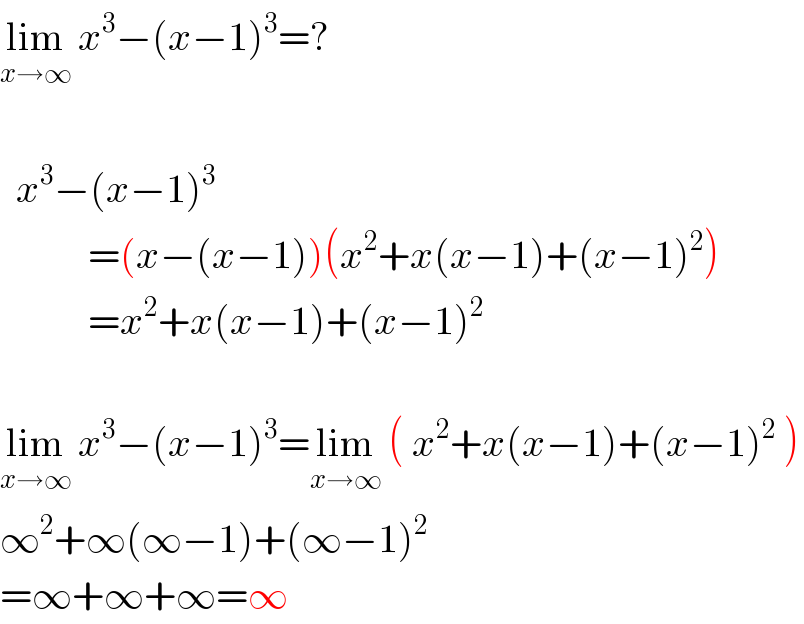
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} =? \\ $$$$ \\ $$$$\:\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left({x}−\left({x}−\mathrm{1}\right)\right)\left({x}^{\mathrm{2}} +{x}\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +{x}\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{3}} −\left({x}−\mathrm{1}\right)^{\mathrm{3}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\:{x}^{\mathrm{2}} +{x}\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:\right) \\ $$$$\infty^{\mathrm{2}} +\infty\left(\infty−\mathrm{1}\right)+\left(\infty−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\infty+\infty+\infty=\infty \\ $$
Commented by Rasheed Soomro last updated on 27/Jun/16
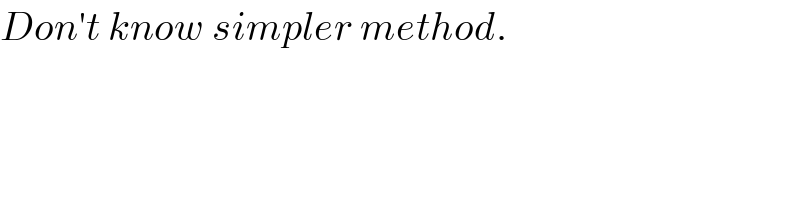
$${Don}'{t}\:{know}\:{simpler}\:{method}. \\ $$
