
Question Number 218076 by malwan last updated on 28/Mar/25

$${How}\:{many}\:{ways}\:{to}\:{arrnge} \\ $$$${the}\:{letters}\:{ABCCCDEFG} \\ $$$$\left(\mathrm{1}\right)\:{in}\:{general}\:. \\ $$$$\left(\mathrm{2}\right)\:{all}\:\mathrm{3}\:{Cs}\:{must}\:{be}\:{together} \\ $$$$\left(\mathrm{3}\right)\:{only}\:\mathrm{2}\:{Cs}\:{must}\:{be}\:{together} \\ $$$$\left(\mathrm{4}\right)\:{no}\:\mathrm{2}\:{or}\:\mathrm{3}\:{Cs}\:{be}\:{together} \\ $$$$\left(\mathrm{5}\right)\:{no}\:{letter}\:{still}\:\:{in}\:{its} \\ $$$${original}\:{place}\:. \\ $$
Answered by efronzo1 last updated on 29/Mar/25

$$\left(\mathrm{1}\right)\:\frac{\mathrm{9}!}{\mathrm{3}!}\: \\ $$$$\left(\mathrm{2}\right)\:\mathrm{7}! \\ $$
Answered by mr W last updated on 29/Mar/25

$$\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{9}!}{\mathrm{3}!}=\mathrm{60480} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{7}!=\mathrm{5040}\: \\ $$$${or}\:\mathrm{6}!×\mathrm{7}=\mathrm{5040} \\ $$$$ \\ $$$$\left(\mathrm{3}\right) \\ $$$$\Box{A}\Box{B}\Box{D}\Box{E}\Box{F}\Box{G}\Box \\ $$$$\mathrm{6}!×\mathrm{7}×\mathrm{6}=\mathrm{30240} \\ $$$${the}\:{two}\:{Cs}\:{and}\:{a}\:{C}\:{must}\:{be}\:{separated}\: \\ $$$${by}\:{other}\:{letters}.\:\:{they}\:{can}\:{be}\:{placed}\: \\ $$$${into}\:{the}\:\mathrm{7}\:{red}\:{boxes}. \\ $$$${to}\:{arrange}\:{the}\:\mathrm{6}\:{other}\:{letters},\:{there} \\ $$$${are}\:\mathrm{6}!\:{ways},\:{to}\:{place}\:{two}\:{Cs}\:{and}\:{a}\:{C}, \\ $$$${there}\:{are}\:\mathrm{7}×\mathrm{6}\:{ways}. \\ $$$${totally}\:\mathrm{6}!×\mathrm{7}×\mathrm{6} \\ $$$$ \\ $$$$\left(\mathrm{4}\right) \\ $$$$\mathrm{6}!×\mathrm{7}×\mathrm{6}×\mathrm{5}/\mathrm{3}!=\mathrm{25200} \\ $$$${see}\:{also}\:{above}.\:{the}\:{three}\:{Cs}\:{must} \\ $$$${be}\:{separated}\:{by}\:{the}\:{other}\:{letters}. \\ $$$${to}\:{place}\:{the}\:{three}\:{Cs}\:{into}\:{the}\:\mathrm{7} \\ $$$${boxes},\:{there}\:{are}\:{C}_{\mathrm{7}} ^{\mathrm{3}} \:=\mathrm{7}×\mathrm{6}×\mathrm{5}/\mathrm{3}! \\ $$$${ways}. \\ $$$${totally}\:\mathrm{6}!×\mathrm{7}×\mathrm{6}×\mathrm{5}/\mathrm{3}! \\ $$$$ \\ $$$$\left(\mathrm{5}\right) \\ $$$${ABCCCDEFG} \\ $$$${EFABDGCCC} \\ $$$${C}_{\mathrm{6}} ^{\mathrm{3}} ×\mathrm{3}!×\left(\frac{\mathrm{6}!}{\mathrm{3}!}−\mathrm{1}−\mathrm{3}×\mathrm{3}−\mathrm{3}×\mathrm{13}\right)=\mathrm{8520} \\ $$$${under}\:{the}\:{three}\:{Cs}\:{other}\:{letters} \\ $$$${must}\:{be}\:{placed}.\:{to}\:{select}\:\mathrm{3}\:{letters} \\ $$$${and}\:{place}\:{them}\:{under}\:{the}\:{Cs}\:{there} \\ $$$${are}\:{C}_{\mathrm{6}} ^{\mathrm{3}} ×\mathrm{3}!=\mathrm{120}\:{ways}.\:{say} \\ $$$${A},{B},{D}\:{are}\:{selected}.\:{to}\:{arrange}\:{the} \\ $$$${remaining}\:\mathrm{6}\:{letters}\:\left({eg}.\:{EFGCCC}\right) \\ $$$${there}\:{are}\:{totally}\:\frac{\mathrm{6}!}{\mathrm{3}!}\:{ways}.\:{but}\:{there} \\ $$$${are}\:{arrangements}\:{in}\:{which}\:{EFG} \\ $$$${are}\:{placed}\:{under}\:{themselves}. \\ $$$${all}\:{three}\:{letters}\:\left({EFG}\right)\:{are}\:{in}\:{false} \\ $$$${positions}:\:{there}\:{is}\:{one}\:{possibility}. \\ $$$${two}\:{letters}\:\left({eg}.\:{EF}\right)\:{are}\:{in}\:{false} \\ $$$${positions}:\:{there}\:{are}\:\mathrm{3}×\mathrm{4}\:{possibilities}. \\ $$$${but}\:{this}\:{also}\:{includes}\:\mathrm{3}\:{times}\:{the} \\ $$$${case}\:{from}\:{above}.\:{that}\:{means}\:{there} \\ $$$${are}\:\mathrm{3}×\mathrm{3}\:{possibilities}\:{for}\:{only}\:{two} \\ $$$${letters}\:{in}\:{false}\:{positions}. \\ $$$${one}\:{letter}\:\left({eg}.\:{E}\right)\:{in}\:{false}\:{position}: \\ $$$${there}\:{are}\:\mathrm{3}×\mathrm{5}×\mathrm{4}\:{possibilities}.\:{but} \\ $$$${this}\:{also}\:{includes}\:\mathrm{7}\:{times}\:{the}\: \\ $$$${cases}\:{above}.\:{that}\:{means}\:{there}\:{are} \\ $$$$\mathrm{3}×\mathrm{13}\:{possibilities}\:{for}\:{only}\:{one} \\ $$$${letter}\:{in}\:{false}\:{position}. \\ $$$${totally}\:{C}_{\mathrm{6}} ^{\mathrm{3}} ×\mathrm{3}!×\left(\frac{\mathrm{6}!}{\mathrm{3}!}−\mathrm{1}−\mathrm{3}×\mathrm{3}−\mathrm{3}×\mathrm{13}\right) \\ $$
Commented by malwan last updated on 29/Mar/25
$${thanks}\:{alot}\:,\:{mr}\:{W}\: \\ $$
Commented by mr W last updated on 29/Mar/25
$${i}'{ve}\:{added}\:{some}\:{explanation}.\: \\ $$
Commented by malwan last updated on 29/Mar/25
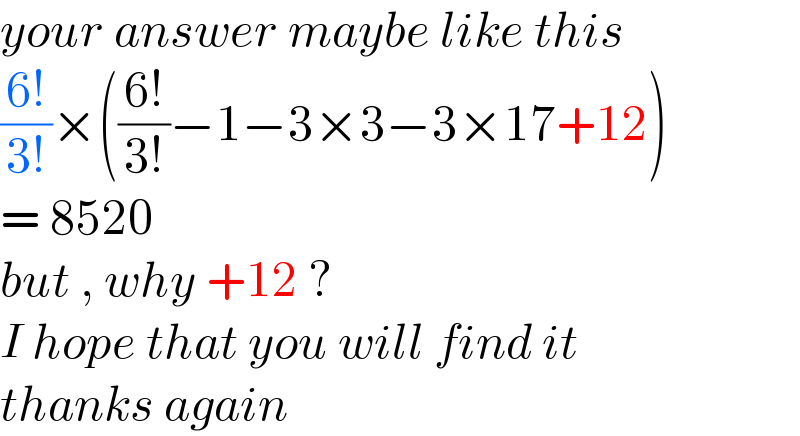
$${your}\:{answer}\:{maybe}\:{like}\:{this} \\ $$$$\frac{\mathrm{6}!}{\mathrm{3}!}×\left(\frac{\mathrm{6}!}{\mathrm{3}!}−\mathrm{1}−\mathrm{3}×\mathrm{3}−\mathrm{3}×\mathrm{17}+\mathrm{12}\right) \\ $$$$=\:\mathrm{8520} \\ $$$${but}\:,\:{why}\:+\mathrm{12}\:? \\ $$$${I}\:{hope}\:{that}\:{you}\:{will}\:{find}\:{it} \\ $$$${thanks}\:{again}\:\:\cancel{\lesseqgtr} \\ $$
Commented by mr W last updated on 29/Mar/25

$${answer}\:{for}\:\left(\mathrm{5}\right)\:{can}\:{also}\:{be}\:{determined} \\ $$$${applying}\:``{rook}\:{polynomial}'' \\ $$$$\frac{\mathrm{51120}}{\mathrm{3}!}=\mathrm{8520} \\ $$
Commented by mr W last updated on 29/Mar/25

Commented by mr W last updated on 29/Mar/25
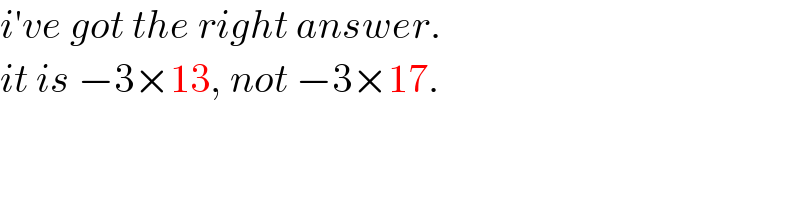
$${i}'{ve}\:{got}\:{the}\:{right}\:{answer}. \\ $$$${it}\:{is}\:−\mathrm{3}×\mathrm{13},\:{not}\:−\mathrm{3}×\mathrm{17}. \\ $$
Commented by malwan last updated on 29/Mar/25
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$$$\:\underline{\underbrace{ }} \\ $$
Commented by mr W last updated on 30/Mar/25

$${this}\:{is}\:{the}\:{explanation}\:{for}\:{why}\: \\ $$$$−\mathrm{3}×\mathrm{13}: \\ $$$${say}\:{we}\:{have}\:{placed}\:{ABD}\:{under}\:{CCC} \\ $$$${ABCCCDEFG} \\ $$$$\Box\Box{ABD}\Box\Box\Box\Box \\ $$$${now}\:{we}\:{try}\:{to}\:{place}\:{EFGCCC}\:{into} \\ $$$${the}\:\mathrm{6}\:{boxes}.\:{totally}\:{there}\:{are}\:\frac{\mathrm{6}!}{\mathrm{3}!}\: \\ $$$${ways}.\:{but}\:{they}\:{include}\:{also}\:{following} \\ $$$${cases}: \\ $$$$\left.\mathrm{1}\right)\:{all}\:{EFG}\:{in}\:{false}\:{positions} \\ $$$${CCABDC}\underline{{EFG}} \\ $$$$\Rightarrow{just}\:{one}\:{time} \\ $$$$\left.\mathrm{2}\right)\:{only}\:{two}\:{of}\:{EFG}\:{in}\:{false}\:{positions} \\ $$$${i}.{e}.\:{EG}\:{or}\:{EG}\:{or}\:{FG}\:{in}\:{false}\:{positions} \\ $$$${say}\:{EG}\:{in}\:{false}\:{positions}: \\ $$$$\Box\Box{ABD}\Box\underline{{EF}}\blacksquare \\ $$$${G}\:{can}\:{be}\:{in}\:{white}\:{boxes},\:\mathrm{3}\:{possibilities}. \\ $$$${totally}\:\mathrm{3}×\mathrm{3}\:{possibilities}. \\ $$$$\left.\mathrm{3}\right)\:{only}\:{one}\:{of}\:{EFG}\:{in}\:{false}\:{position} \\ $$$${i}.{e}.\:{E}\:{or}\:{F}\:{or}\:{G}\:{in}\:{false}\:{position} \\ $$$${say}\:{E}\:{in}\:{false}\:{position}: \\ $$$$\Box\Box{ABD}\Box\underline{{E}}\Box\Box \\ $$$${there}\:{are}\:\mathrm{5}×\mathrm{4}=\mathrm{20}\:{possibilities} \\ $$$${to}\:{place}\:{FG}\:{and}\:{Cs}.\:{but}\:{this}\:{includes}\: \\ $$$$\Box\Box{ABD}\Box\underline{{EFG}}\:\Rightarrow\mathrm{1}\:{time} \\ $$$$\Box\Box{ABD}\Box\underline{{EF}}\blacksquare\:\Rightarrow\mathrm{3}\:{times}\:\left({G}\:{in}\:\Box\right) \\ $$$$\Box\Box{ABD}\Box\underline{{E}}\blacksquare\underline{{G}}\:\Rightarrow\mathrm{3}\:{times}\:\left({F}\:{in}\:\Box\right) \\ $$$${therefore}\:{we}\:{have}\:\mathrm{20}−\mathrm{7}=\mathrm{13}\:{cases} \\ $$$${with}\:{only}\:{E}\:{in}\:{false}\:{position}. \\ $$
Commented by malwan last updated on 31/Mar/25
$${Thank}\:{you}\:{trillion}\:\:\cancel{\lesseqgtr} \\ $$
