
Question Number 5796 by FilupSmith last updated on 28/May/16

$$\mathrm{How}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{you}\:\mathrm{express} \\ $$$$\mathrm{30},\mathrm{030}\:\mathrm{as}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{4}\:\mathrm{positive}\:\mathrm{numbers}? \\ $$$$\left(\mathrm{excluding}\:\mathrm{1}\right) \\ $$
Commented by Rasheed Soomro last updated on 28/May/16
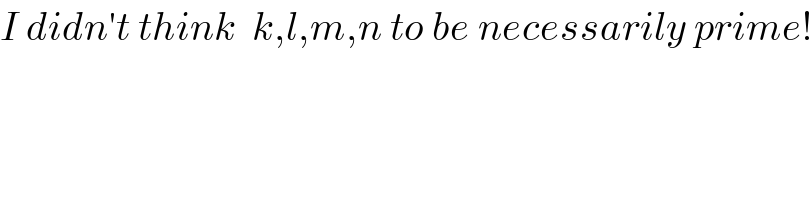
$${I}\:{didn}'{t}\:{think}\:\:{k},{l},{m},{n}\:{to}\:{be}\:{necessarily}\:{prime}! \\ $$
Commented by FilupSmith last updated on 28/May/16

$${ok}\:{so} \\ $$$${x}\:\mathrm{as}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{can}\:\mathrm{be}\:\mathrm{split}\:\mathrm{into}\:\mathrm{a}\:\mathrm{maximum} \\ $$$$\mathrm{amount}\:\mathrm{of}\:\mathrm{products}\:\mathrm{as}\:\mathrm{its}\:\mathrm{prime}\:\mathrm{factors}. \\ $$$$\mathrm{eg}.\:\mathrm{100}=\mathrm{2}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} =\mathrm{2}×\mathrm{2}×\mathrm{5}×\mathrm{5} \\ $$$$\mathrm{so}\:\mathrm{100}\:\mathrm{can}\:\mathrm{be}\:\mathrm{split}\:\mathrm{to}\:\mathrm{a}\:\mathrm{max}\:\mathrm{of}\:\mathrm{4}\:\mathrm{numbers} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{ylu}\:\mathrm{can}\:\mathrm{express}\:\mathrm{100} \\ $$$$\mathrm{as}\:\mathrm{4}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{4}!=\mathrm{24}\:\mathrm{ways} \\ $$$$\mathrm{100}=\mathrm{2}×\mathrm{2}×\mathrm{5}×\mathrm{5}=\mathrm{5}×\mathrm{5}×\mathrm{2}×\mathrm{2}=...\mathrm{etc} \\ $$$$ \\ $$$$\mathrm{to}\:\mathrm{look}\:\mathrm{at}\:\mathrm{combinatioms}\:\mathrm{of}\:\mathrm{3}\:\mathrm{it}\:\mathrm{is}\:^{\mathrm{4}} \mathrm{C}_{\mathrm{3}} \\ $$$$\boldsymbol{{PLUS}}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{you}\:\mathrm{can}\:\mathrm{turn} \\ $$$$\mathrm{2}×\mathrm{2}×\mathrm{5}×\mathrm{5}\:\mathrm{into}\:\mathrm{3}\:\mathrm{numbers}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{2}×\mathrm{2}×\mathrm{5}×\mathrm{5}: \\ $$$${a}_{\mathrm{1}} =\mathrm{4}×\mathrm{5}×\mathrm{5}\:\:\:\:\:\:{a}_{\mathrm{2}} =\mathrm{5}×\mathrm{4}×\mathrm{5}\:\:\:\:{a}_{\mathrm{3}} =... \\ $$$${a}_{\mathrm{4}} =\mathrm{2}×\mathrm{10}×\mathrm{2}\:\:\:\:...{etc}\:\:{a}_{{n}} =... \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{that}\:=\:{n} \\ $$$$\therefore\:\mathrm{combinations}\:\mathrm{of}\:\mathrm{3}=^{\mathrm{4}} {C}_{\mathrm{3}} +{n} \\ $$$$ \\ $$$${thoughts}\:{or}\:{simplifications}? \\ $$
Commented by FilupSmith last updated on 28/May/16
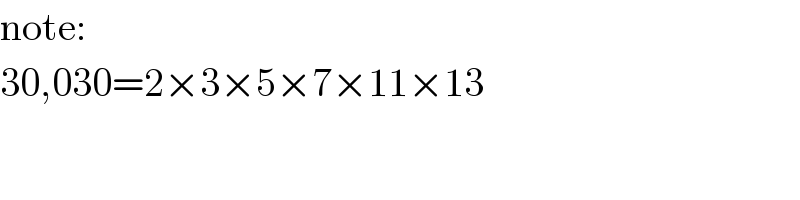
$$\mathrm{note}: \\ $$$$\mathrm{30},\mathrm{030}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13} \\ $$
Commented by Rasheed Soomro last updated on 29/May/16

$$\mathrm{30},\mathrm{030}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13}\:\left({total}\:{factors}\:\mathrm{6}\right) \\ $$$$\mathcal{A}{ctually}\:{we}\:{have}\:{to}\:\:{divide}\:{above}\:\mathrm{6}\:{primes} \\ $$$${into}\:{four}\:\:{groups}\:{whose}\:{products} \\ $$$${will}\:{be}\:{required}\:{four}\:{positive}\:{numbers}. \\ $$$${Two}\:{cases}\:{are}\:{possible}. \\ $$$$ \\ $$$$\mathcal{C}{ase}-{I}\::\:\mathcal{W}{hen}\:{groups}\:{contain}\:\mathrm{3},\mathrm{1},\mathrm{1},\mathrm{1}\:{primes} \\ $$$$\:\:\:^{\mathrm{6}} \mathrm{C}_{\mathrm{3}} =\frac{\mathrm{6}×\mathrm{5}×\mathrm{4}}{\mathrm{1}×\mathrm{2}×\mathrm{3}}=\mathrm{20}\:\mathrm{ways} \\ $$$$\mathcal{C}{ase}-{II}\::\:\mathcal{W}{hen}\:{groups}\:{contain}\:\mathrm{2},\mathrm{2},\mathrm{1},\mathrm{1}\:{primes} \\ $$$$\:\:\:\:\:\:^{\mathrm{6}} \mathrm{C}_{\mathrm{2}} ×^{\mathrm{4}} \mathrm{C}_{\mathrm{2}} =\frac{\mathrm{6}×\mathrm{5}}{\mathrm{1}×\mathrm{2}}×\frac{\mathrm{4}×\mathrm{3}}{\mathrm{1}×\mathrm{2}}=\mathrm{15}×\mathrm{6}=\mathrm{90}\:\mathrm{ways} \\ $$$$\mathrm{Total}\:\mathrm{ways}\:\mathrm{in}\:\mathrm{which}\:\mathrm{the}\:\mathrm{number}\:\mathrm{can}\:\mathrm{be}\: \\ $$$$\mathrm{expressed}\:\mathrm{as}\:\mathrm{product}\:\mathrm{of}\:\mathrm{four}\:\mathrm{positive}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{20}+\mathrm{90}=\mathrm{110} \\ $$$${Remember}\:{that}\:{order}\:{of}\:{number}\:\:{is}\:{not}\:{important}. \\ $$$${And}\:\:{if}\:\:{order}\:{is}\:{important}\:{then}\:{number}\:{of}\:{ways} \\ $$$$=\mathrm{110}×\mathrm{4}!=\mathrm{2640} \\ $$$${I}\:{am}\:{not}\:{confident}. \\ $$$${prakashjain},\:{Yozzi}\:{and}\:\:{others}\:{can}\:{help}\:{me}. \\ $$
Commented by FilupSmith last updated on 28/May/16

$$\mathrm{One}\:\mathrm{thing}\:\mathrm{to}\:\mathrm{consider}\:\mathrm{is}\:\mathrm{that} \\ $$$$\mathrm{30030}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}×\mathrm{15}×\mathrm{7}×\mathrm{11}×\mathrm{13} \\ $$$$\mathrm{etc}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{30}×\mathrm{7}×\mathrm{11}×\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}×\mathrm{35}×\mathrm{11}×\mathrm{13} \\ $$$$\mathrm{etc}. \\ $$$$ \\ $$$${i}.{e}.\:{k},\:{l},\:{m},\:{n}\:\:\:\mathrm{dont}\:\mathrm{have}\:\mathrm{to}\:\mathrm{be}\:\mathrm{prime} \\ $$$$\mathrm{the}\:\mathrm{trick},\:\mathrm{i}\:\mathrm{think},\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{combinations} \\ $$$$\mathrm{of}\:\mathrm{products},\:\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{combination} \\ $$$$\mathrm{out}\:\mathrm{of}\:\mathrm{each}\:\mathrm{one}. \\ $$
Commented by Rasheed Soomro last updated on 29/May/16

$${As}\:{the}\:{order}\:{doesn}'{t}\:{matter}\:{in}\:{multiplication} \\ $$$${so}\:{I}\:{considered}\:\mathrm{6}×\mathrm{5}×\mathrm{77}×\mathrm{13}\:\:{and}\:\mathrm{13}×\mathrm{5}×\mathrm{6}×\mathrm{77} \\ $$$${same}.{And}\:{this}\:{is}\:{what}\:{I}\:{have}\:{understood}\:{from} \\ $$$${the}\:{question}.\:{Anyway}\:{if}\:{we}\:{had}\:{an}\:{answer} \\ $$$${in}\:{which}\:{order}\:{is}\:{not}\:{considered}\:{important}\:{then} \\ $$$${change}\:{it}\:{in}\:{answer}\:{in}\:{which}\:{order}\:{is}\:{importanyt} \\ $$$${is}\:{very}\:{simple}! \\ $$
