Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 118694 by benjo_mathlover last updated on 19/Oct/20

How many sets of 3 numbers each can be formed from the numbers { 1,2,3,...,20 } if no two consecutive numbers are to be in a set ?

$${How}\:{many}\:{sets}\:{of}\:\mathrm{3}\:{numbers}\:{each}\:{can} \\ $$$${be}\:{formed}\:{from}\:{the}\:{numbers}\:\left\{\:\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{20}\:\right\}\:{if}\:{no} \\ $$$${two}\:{consecutive}\:{numbers}\:{are}\:{to}\:{be}\:{in}\:{a}\:{set}\:? \\ $$

Answered by bemath last updated on 19/Oct/20

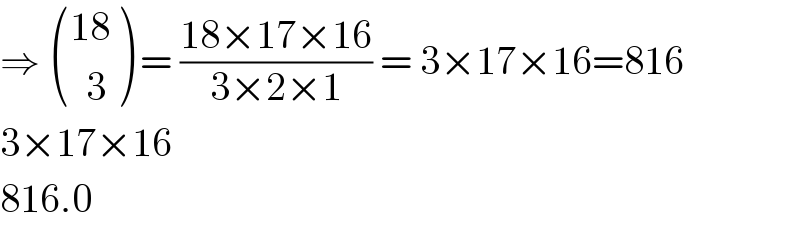
⇒ (((18)),(( 3)) ) = ((18×17×16)/(3×2×1)) = 3×17×16=816 3×17×16 816.0

$$\Rightarrow\:\begin{pmatrix}{\mathrm{18}}\\{\:\:\mathrm{3}}\end{pmatrix}\:=\:\frac{\mathrm{18}×\mathrm{17}×\mathrm{16}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}\:=\:\mathrm{3}×\mathrm{17}×\mathrm{16}=\mathrm{816} \\ $$$$\mathrm{3}×\mathrm{17}×\mathrm{16} \\ $$$$\mathrm{816}.\mathrm{0} \\ $$

Commented by benjo_mathlover last updated on 19/Oct/20

yes correct

$${yes}\:{correct} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/Oct/20

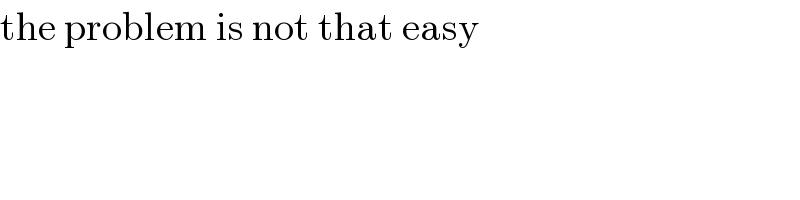
the problem is not that easy

$$\mathrm{the}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{not}\:\mathrm{that}\:\mathrm{easy} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/Oct/20

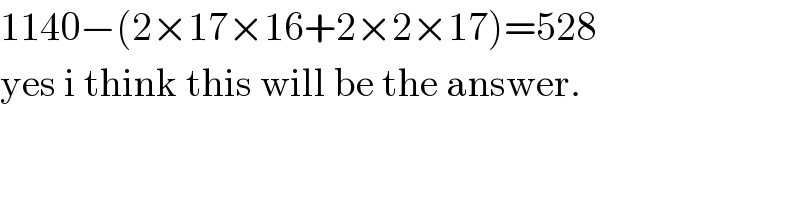
1140−(2×17×16+2×2×17)=528 yes i think this will be the answer.

$$\mathrm{1140}−\left(\mathrm{2}×\mathrm{17}×\mathrm{16}+\mathrm{2}×\mathrm{2}×\mathrm{17}\right)=\mathrm{528}\: \\ $$$$\mathrm{yes}\:\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{answer}. \\ $$

Answered by mr W last updated on 19/Oct/20

total: C_3 ^(20) three consecutive numbers: 1+2+3, 2+3+4,...,18+19+20 ⇒18 two consecutive numbers: 1+2: 17 2+3: 16 3+4: 16 ... 18+19: 16 19+20: 17 ⇒2×17+17×16=17×18 totally: C_3 ^(20) −18−17×18=816

$${total}:\:{C}_{\mathrm{3}} ^{\mathrm{20}} \\ $$$$ \\ $$$${three}\:{consecutive}\:{numbers}:\: \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3},\:\mathrm{2}+\mathrm{3}+\mathrm{4},...,\mathrm{18}+\mathrm{19}+\mathrm{20} \\ $$$$\Rightarrow\mathrm{18} \\ $$$$ \\ $$$${two}\:{consecutive}\:{numbers}:\: \\ $$$$\mathrm{1}+\mathrm{2}:\:\mathrm{17} \\ $$$$\mathrm{2}+\mathrm{3}:\:\mathrm{16} \\ $$$$\mathrm{3}+\mathrm{4}:\:\mathrm{16} \\ $$$$... \\ $$$$\mathrm{18}+\mathrm{19}:\:\mathrm{16} \\ $$$$\mathrm{19}+\mathrm{20}:\:\mathrm{17} \\ $$$$\Rightarrow\mathrm{2}×\mathrm{17}+\mathrm{17}×\mathrm{16}=\mathrm{17}×\mathrm{18} \\ $$$$ \\ $$$${totally}: \\ $$$${C}_{\mathrm{3}} ^{\mathrm{20}} −\mathrm{18}−\mathrm{17}×\mathrm{18}=\mathrm{816} \\ $$

Commented by benjo_mathlover last updated on 20/Oct/20

yes...

$${yes}... \\ $$

Commented by PRITHWISH SEN 2 last updated on 20/Oct/20

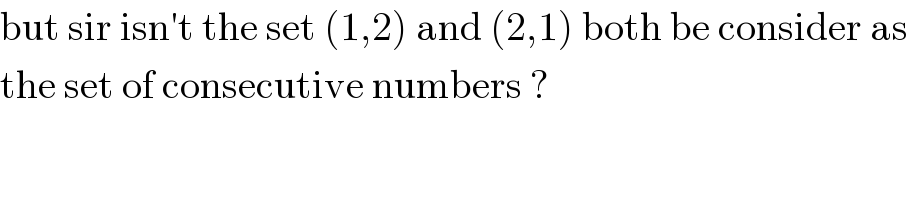
but sir isn′t the set (1,2) and (2,1) both be consider as the set of consecutive numbers ?

$$\mathrm{but}\:\mathrm{sir}\:\mathrm{isn}'\mathrm{t}\:\mathrm{the}\:\mathrm{set}\:\left(\mathrm{1},\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{2},\mathrm{1}\right)\:\mathrm{both}\:\mathrm{be}\:\mathrm{consider}\:\mathrm{as} \\ $$$$\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{consecutive}\:\mathrm{numbers}\:? \\ $$

Commented by mr W last updated on 20/Oct/20

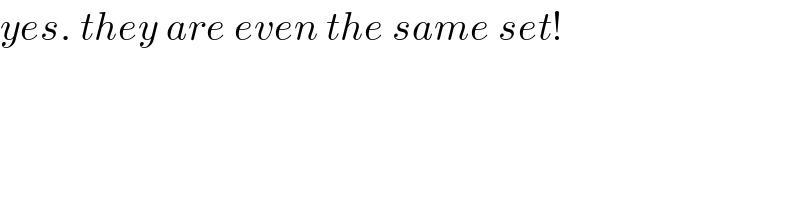
yes. they are even the same set!

$${yes}.\:{they}\:{are}\:{even}\:{the}\:{same}\:{set}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com