
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 203833 by depressiveshrek last updated on 29/Jan/24
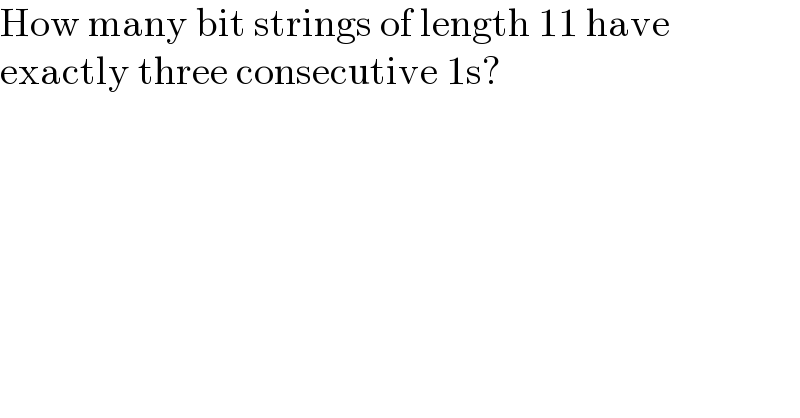
$$\mathrm{How}\:\mathrm{many}\:\mathrm{bit}\:\mathrm{strings}\:\mathrm{of}\:\mathrm{length}\:\mathrm{11}\:\mathrm{have} \\ $$$$\mathrm{exactly}\:\mathrm{three}\:\mathrm{consecutive}\:\mathrm{1s}? \\ $$
Answered by nikif99 last updated on 30/Jan/24

$${Such}\:{a}\:{typical}\:{bit}\:{string}\:{of}\:{length}=\mathrm{11}\:{is} \\ $$$$\mathrm{000}\underset{{pos}=\mathrm{4}} {\underbrace{\mathrm{111}}00000} \\ $$$${Cases}\:{of}\:{positioning}\:'\mathrm{111}'\:{are}\:\mathrm{9} \\ $$$${starting}\:{at}\:{positions}\:\mathrm{1}−\mathrm{9}. \\ $$
