Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 178395 by mr W last updated on 16/Oct/22

How many 5 digit numbers with different digits are multiple of 9?

$${How}\:{many}\:\mathrm{5}\:{digit}\:{numbers}\:{with} \\ $$$${different}\:{digits}\:{are}\:{multiple}\:{of}\:\mathrm{9}? \\ $$

Answered by cortano1 last updated on 16/Oct/22

(1)1+5+6+7+8⇒5! (2)1+2+3+4+8⇒5! (3)1+2+4+5+6⇒5! (4)1+2+3+5+7⇒5! (5)1+3+6+8+9⇒5! (6)1+4+5+8+9⇒5! (7)1+2+7+8+9⇒5! (8)2+3+5+8+9⇒5! ⇒8×5!=8×120=960

$$\left(\mathrm{1}\right)\mathrm{1}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{2}\right)\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{8}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{3}\right)\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{5}+\mathrm{6}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{4}\right)\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{5}+\mathrm{7}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{5}\right)\mathrm{1}+\mathrm{3}+\mathrm{6}+\mathrm{8}+\mathrm{9}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{6}\right)\mathrm{1}+\mathrm{4}+\mathrm{5}+\mathrm{8}+\mathrm{9}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{7}\right)\mathrm{1}+\mathrm{2}+\mathrm{7}+\mathrm{8}+\mathrm{9}\Rightarrow\mathrm{5}! \\ $$$$\left(\mathrm{8}\right)\mathrm{2}+\mathrm{3}+\mathrm{5}+\mathrm{8}+\mathrm{9}\Rightarrow\mathrm{5}! \\ $$$$\Rightarrow\mathrm{8}×\mathrm{5}!=\mathrm{8}×\mathrm{120}=\mathrm{960} \\ $$$$ \\ $$

Commented by mr W last updated on 16/Oct/22

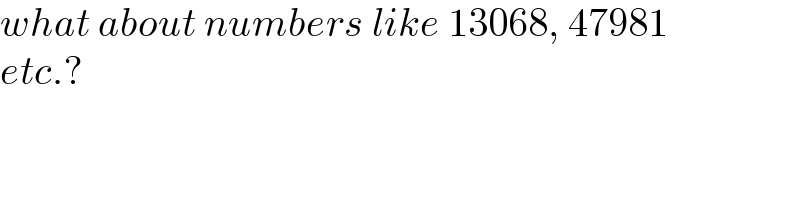
what about numbers like 13068, 47981 etc.?

$${what}\:{about}\:{numbers}\:{like}\:\mathrm{13068},\:\mathrm{47981}\: \\ $$$${etc}.? \\ $$

Commented by Tawa11 last updated on 16/Oct/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 16/Oct/22

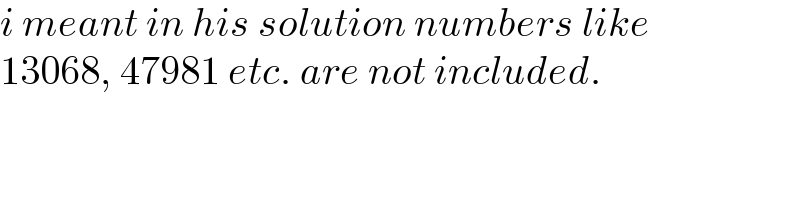
i meant in his solution numbers like 13068, 47981 etc. are not included.

$${i}\:{meant}\:{in}\:{his}\:{solution}\:{numbers}\:{like} \\ $$$$\mathrm{13068},\:\mathrm{47981}\:{etc}.\:{are}\:{not}\:{included}. \\ $$

Commented by mr W last updated on 16/Oct/22

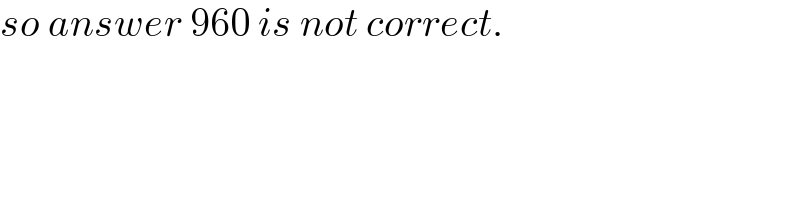
so answer 960 is not correct.

$${so}\:{answer}\:\mathrm{960}\:{is}\:{not}\:{correct}. \\ $$

Commented by cortano1 last updated on 16/Oct/22

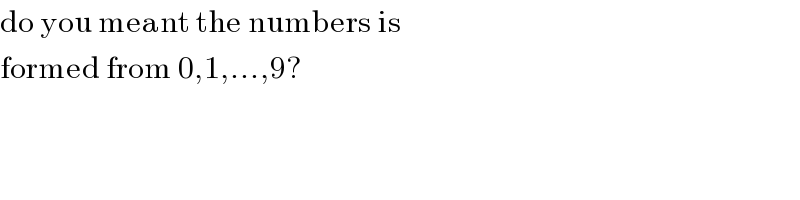
do you meant the numbers is formed from 0,1,...,9?

$$\mathrm{do}\:\mathrm{you}\:\mathrm{meant}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{is} \\ $$$$\mathrm{formed}\:\mathrm{from}\:\mathrm{0},\mathrm{1},...,\mathrm{9}? \\ $$

Commented by mr W last updated on 16/Oct/22

yes. all digits are allowed.

$${yes}.\:{all}\:{digits}\:{are}\:{allowed}. \\ $$

Commented by cortano1 last updated on 16/Oct/22

ok sir

$$\mathrm{ok}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 16/Oct/22

typo. it′s just an example.

$${typo}.\:{it}'{s}\:{just}\:{an}\:{example}. \\ $$

Commented by cortano1 last updated on 16/Oct/22

what your answer sir?

$$\mathrm{what}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 16/Oct/22

i got 3024.

$${i}\:{got}\:\mathrm{3024}. \\ $$

Answered by mr W last updated on 16/Oct/22

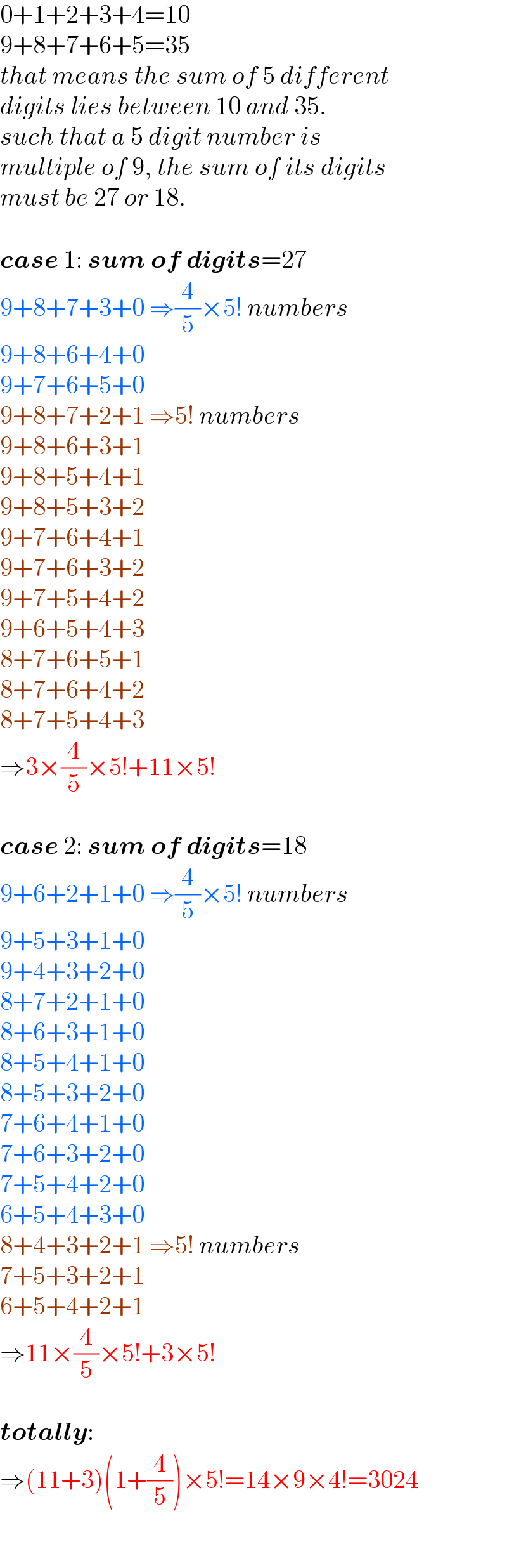
0+1+2+3+4=10 9+8+7+6+5=35 that means the sum of 5 different digits lies between 10 and 35. such that a 5 digit number is multiple of 9, the sum of its digits must be 27 or 18. case 1: sum of digits=27 9+8+7+3+0 ⇒(4/5)×5! numbers 9+8+6+4+0 9+7+6+5+0 9+8+7+2+1 ⇒5! numbers 9+8+6+3+1 9+8+5+4+1 9+8+5+3+2 9+7+6+4+1 9+7+6+3+2 9+7+5+4+2 9+6+5+4+3 8+7+6+5+1 8+7+6+4+2 8+7+5+4+3 ⇒3×(4/5)×5!+11×5! case 2: sum of digits=18 9+6+2+1+0 ⇒(4/5)×5! numbers 9+5+3+1+0 9+4+3+2+0 8+7+2+1+0 8+6+3+1+0 8+5+4+1+0 8+5+3+2+0 7+6+4+1+0 7+6+3+2+0 7+5+4+2+0 6+5+4+3+0 8+4+3+2+1 ⇒5! numbers 7+5+3+2+1 6+5+4+2+1 ⇒11×(4/5)×5!+3×5! totally: ⇒(11+3)(1+(4/5))×5!=14×9×4!=3024

$$\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}=\mathrm{10} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{7}+\mathrm{6}+\mathrm{5}=\mathrm{35} \\ $$$${that}\:{means}\:{the}\:{sum}\:{of}\:\mathrm{5}\:{different} \\ $$$${digits}\:{lies}\:{between}\:\mathrm{10}\:{and}\:\mathrm{35}.\: \\ $$$${such}\:{that}\:{a}\:\mathrm{5}\:{digit}\:{number}\:{is}\: \\ $$$${multiple}\:{of}\:\mathrm{9},\:{the}\:{sum}\:{of}\:{its}\:{digits}\: \\ $$$${must}\:{be}\:\mathrm{27}\:{or}\:\mathrm{18}. \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{1}:\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{digits}}=\mathrm{27} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{7}+\mathrm{3}+\mathrm{0}\:\Rightarrow\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{5}!\:{numbers} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{6}+\mathrm{4}+\mathrm{0} \\ $$$$\mathrm{9}+\mathrm{7}+\mathrm{6}+\mathrm{5}+\mathrm{0} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{7}+\mathrm{2}+\mathrm{1}\:\Rightarrow\mathrm{5}!\:{numbers} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{6}+\mathrm{3}+\mathrm{1} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{5}+\mathrm{4}+\mathrm{1} \\ $$$$\mathrm{9}+\mathrm{8}+\mathrm{5}+\mathrm{3}+\mathrm{2} \\ $$$$\mathrm{9}+\mathrm{7}+\mathrm{6}+\mathrm{4}+\mathrm{1} \\ $$$$\mathrm{9}+\mathrm{7}+\mathrm{6}+\mathrm{3}+\mathrm{2} \\ $$$$\mathrm{9}+\mathrm{7}+\mathrm{5}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{9}+\mathrm{6}+\mathrm{5}+\mathrm{4}+\mathrm{3} \\ $$$$\mathrm{8}+\mathrm{7}+\mathrm{6}+\mathrm{5}+\mathrm{1} \\ $$$$\mathrm{8}+\mathrm{7}+\mathrm{6}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{8}+\mathrm{7}+\mathrm{5}+\mathrm{4}+\mathrm{3}\: \\ $$$$\Rightarrow\mathrm{3}×\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{5}!+\mathrm{11}×\mathrm{5}! \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{digits}}=\mathrm{18} \\ $$$$\mathrm{9}+\mathrm{6}+\mathrm{2}+\mathrm{1}+\mathrm{0}\:\Rightarrow\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{5}!\:{numbers} \\ $$$$\mathrm{9}+\mathrm{5}+\mathrm{3}+\mathrm{1}+\mathrm{0} \\ $$$$\mathrm{9}+\mathrm{4}+\mathrm{3}+\mathrm{2}+\mathrm{0} \\ $$$$\mathrm{8}+\mathrm{7}+\mathrm{2}+\mathrm{1}+\mathrm{0} \\ $$$$\mathrm{8}+\mathrm{6}+\mathrm{3}+\mathrm{1}+\mathrm{0} \\ $$$$\mathrm{8}+\mathrm{5}+\mathrm{4}+\mathrm{1}+\mathrm{0} \\ $$$$\mathrm{8}+\mathrm{5}+\mathrm{3}+\mathrm{2}+\mathrm{0} \\ $$$$\mathrm{7}+\mathrm{6}+\mathrm{4}+\mathrm{1}+\mathrm{0} \\ $$$$\mathrm{7}+\mathrm{6}+\mathrm{3}+\mathrm{2}+\mathrm{0} \\ $$$$\mathrm{7}+\mathrm{5}+\mathrm{4}+\mathrm{2}+\mathrm{0} \\ $$$$\mathrm{6}+\mathrm{5}+\mathrm{4}+\mathrm{3}+\mathrm{0} \\ $$$$\mathrm{8}+\mathrm{4}+\mathrm{3}+\mathrm{2}+\mathrm{1}\:\Rightarrow\mathrm{5}!\:{numbers} \\ $$$$\mathrm{7}+\mathrm{5}+\mathrm{3}+\mathrm{2}+\mathrm{1} \\ $$$$\mathrm{6}+\mathrm{5}+\mathrm{4}+\mathrm{2}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{11}×\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{5}!+\mathrm{3}×\mathrm{5}! \\ $$$$ \\ $$$$\boldsymbol{{totally}}: \\ $$$$\Rightarrow\left(\mathrm{11}+\mathrm{3}\right)\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{5}}\right)×\mathrm{5}!=\mathrm{14}×\mathrm{9}×\mathrm{4}!=\mathrm{3024} \\ $$

Commented by SLVR last updated on 25/Oct/22

it is more clear...awesom.super

$${it}\:{is}\:{more}\:{clear}...{awesom}.{super} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com