
Question Number 116238 by Ar Brandon last updated on 02/Oct/20

$$\mathrm{How}\:\mathrm{long}\:\mathrm{does}\:\mathrm{it}\:\mathrm{take}\:\mathrm{for}\:\mathrm{the}\:\mathrm{disintegration}\:\mathrm{of} \\ $$$$\frac{\mathrm{3}}{\mathrm{10}}\:\mathrm{of}\:\mathrm{an}\:\mathrm{atom}\:\mathrm{with}\:\mathrm{radioactive}\:\mathrm{constant}\:\lambda\:? \\ $$
Answered by MrGaster last updated on 22/Jan/25
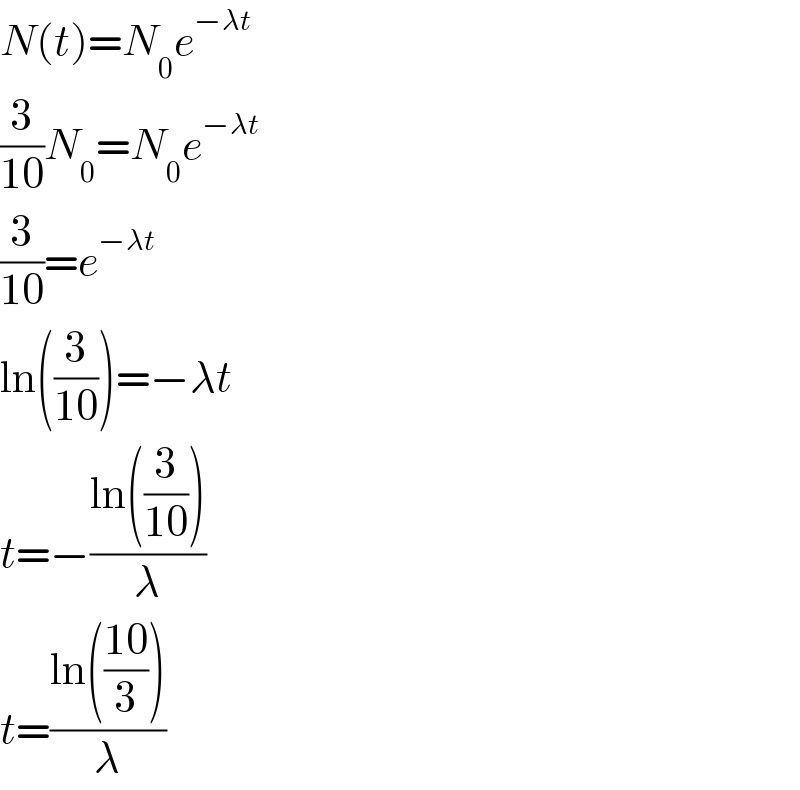
$${N}\left({t}\right)={N}_{\mathrm{0}} {e}^{−\lambda{t}} \\ $$$$\frac{\mathrm{3}}{\mathrm{10}}{N}_{\mathrm{0}} ={N}_{\mathrm{0}} {e}^{−\lambda{t}} \\ $$$$\frac{\mathrm{3}}{\mathrm{10}}={e}^{−\lambda{t}} \\ $$$$\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{10}}\right)=−\lambda{t} \\ $$$${t}=−\frac{\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{10}}\right)}{\lambda} \\ $$$${t}=\frac{\mathrm{ln}\left(\frac{\mathrm{10}}{\mathrm{3}}\right)}{\lambda} \\ $$
