
Question Number 137741 by bemath last updated on 06/Apr/21

$$ \\ $$How do I use the Lagrange multiplier method to find the maximum of the function f(x,y)=4-2x-2y on the curve x^2+y^2=4?
Answered by TheSupreme last updated on 06/Apr/21
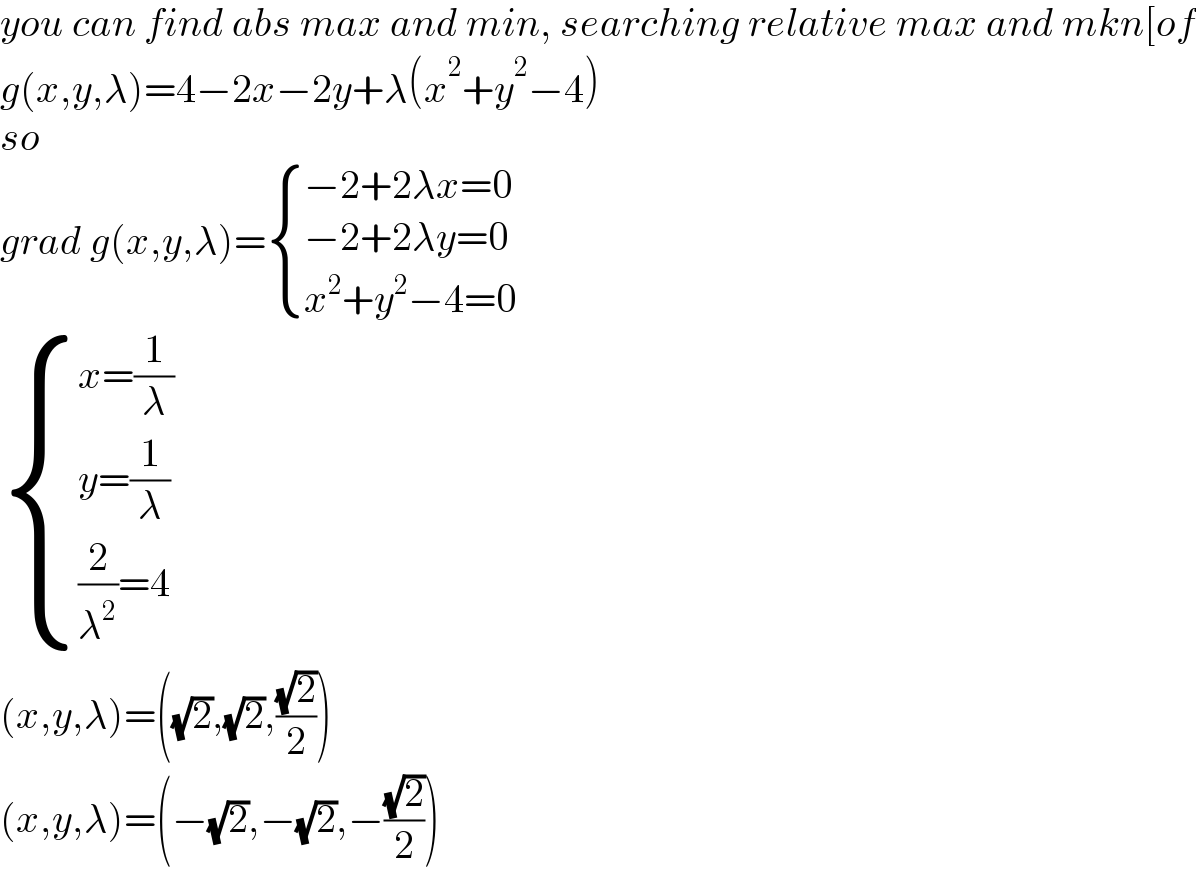
$${you}\:{can}\:{find}\:{abs}\:{max}\:{and}\:{min},\:{searching}\:{relative}\:{max}\:{and}\:{mkn}\left[{of}\right. \\ $$$${g}\left({x},{y},\lambda\right)=\mathrm{4}−\mathrm{2}{x}−\mathrm{2}{y}+\lambda\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$${so}\: \\ $$$${grad}\:{g}\left({x},{y},\lambda\right)=\begin{cases}{−\mathrm{2}+\mathrm{2}\lambda{x}=\mathrm{0}}\\{−\mathrm{2}+\mathrm{2}\lambda{y}=\mathrm{0}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{{x}=\frac{\mathrm{1}}{\lambda}}\\{{y}=\frac{\mathrm{1}}{\lambda}}\\{\frac{\mathrm{2}}{\lambda^{\mathrm{2}} }=\mathrm{4}}\end{cases} \\ $$$$\left({x},{y},\lambda\right)=\left(\sqrt{\mathrm{2}},\sqrt{\mathrm{2}},\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\left({x},{y},\lambda\right)=\left(−\sqrt{\mathrm{2}},−\sqrt{\mathrm{2}},−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$
Answered by mr W last updated on 06/Apr/21
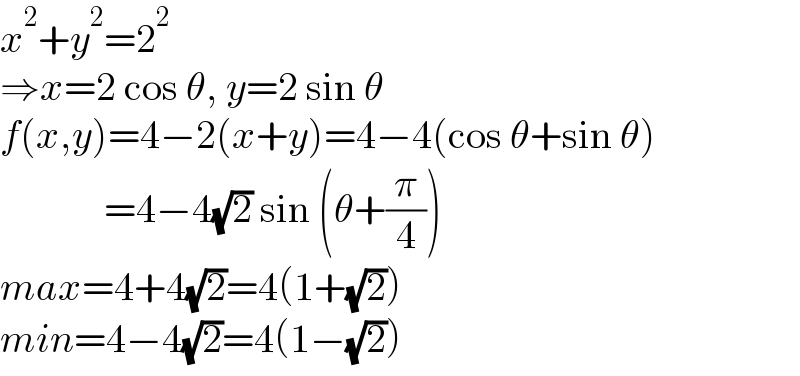
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\mathrm{cos}\:\theta,\:{y}=\mathrm{2}\:\mathrm{sin}\:\theta \\ $$$${f}\left({x},{y}\right)=\mathrm{4}−\mathrm{2}\left({x}+{y}\right)=\mathrm{4}−\mathrm{4}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{4}}\right) \\ $$$${max}=\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}=\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${min}=\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}=\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right) \\ $$
