
Question Number 212304 by issac last updated on 09/Oct/24
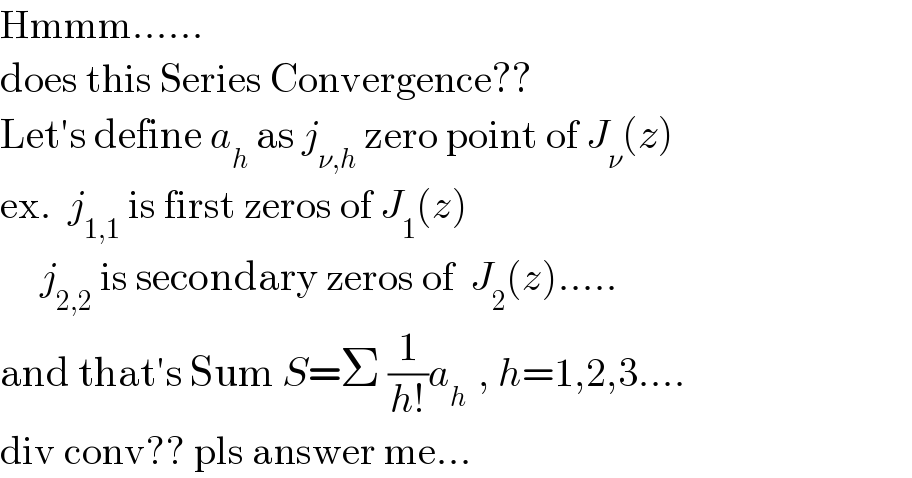
$$\mathrm{Hmmm}...... \\ $$$$\mathrm{does}\:\mathrm{this}\:\mathrm{Series}\:\mathrm{Convergence}?? \\ $$$$\mathrm{Let}'\mathrm{s}\:\mathrm{define}\:{a}_{{h}} \:\mathrm{as}\:{j}_{\nu,{h}} \:\mathrm{zero}\:\mathrm{point}\:\mathrm{of}\:{J}_{\nu} \left({z}\right) \\ $$$$\mathrm{ex}.\:\:{j}_{\mathrm{1},\mathrm{1}} \:\mathrm{is}\:\mathrm{first}\:\mathrm{zeros}\:\mathrm{of}\:{J}_{\mathrm{1}} \left({z}\right) \\ $$$$\:\:\:\:\:{j}_{\mathrm{2},\mathrm{2}} \:\mathrm{is}\:\mathrm{secondary}\:\mathrm{zeros}\:\mathrm{of}\:\:{J}_{\mathrm{2}} \left({z}\right)..... \\ $$$$\mathrm{and}\:\mathrm{that}'\mathrm{s}\:\mathrm{Sum}\:{S}=\Sigma\:\frac{\mathrm{1}}{{h}!}{a}_{{h}\:} \:,\:{h}=\mathrm{1},\mathrm{2},\mathrm{3}.... \\ $$$$\mathrm{div}\:\mathrm{conv}??\:\mathrm{pls}\:\mathrm{answer}\:\mathrm{me}... \\ $$
Commented by Frix last updated on 09/Oct/24

$$\mathrm{What}\:\mathrm{is}\:{J}_{{v}} \left({z}\right)? \\ $$
