Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 212598 by MATHEMATICSAM last updated on 18/Oct/24

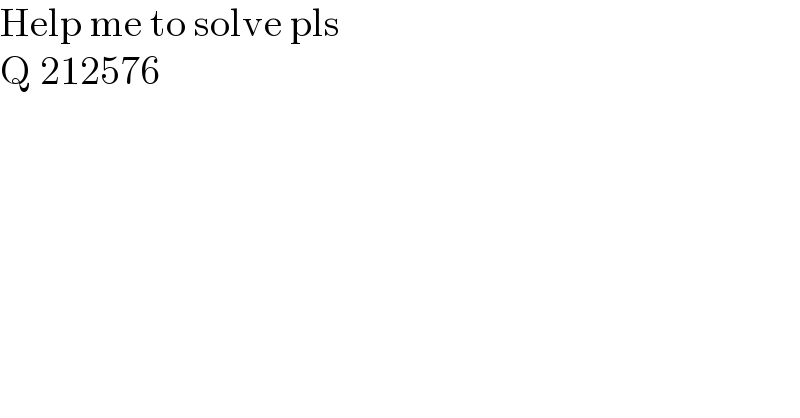
Help me to solve pls Q 212576

$$\mathrm{Help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{pls} \\ $$$$\mathrm{Q}\:\mathrm{212576}\: \\ $$

Answered by A5T last updated on 18/Oct/24

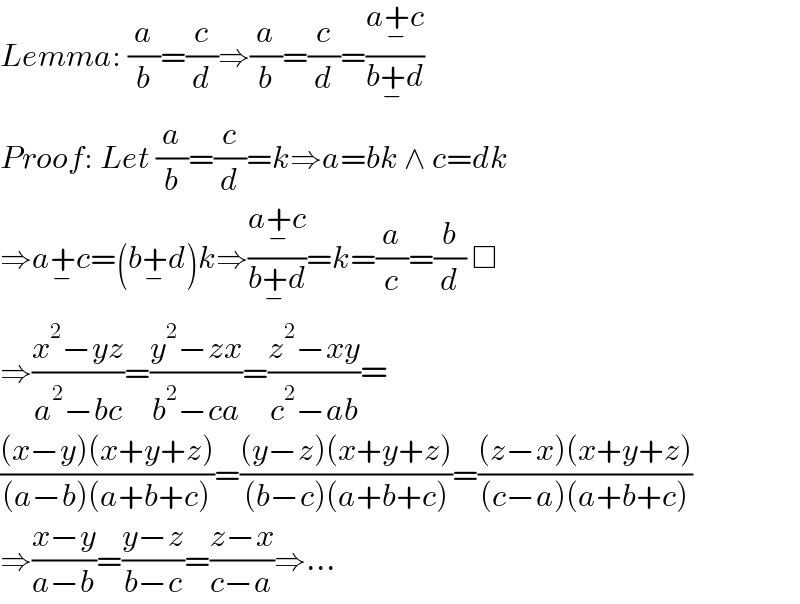
Lemma: (a/b)=(c/d)⇒(a/b)=(c/d)=((a+_− c)/(b+_− d)) Proof: Let (a/b)=(c/d)=k⇒a=bk ∧ c=dk ⇒a+_− c=(b+_− d)k⇒((a+_− c)/(b+_− d))=k=(a/c)=(b/d) □ ⇒((x^2 −yz)/(a^2 −bc))=((y^2 −zx)/(b^2 −ca))=((z^2 −xy)/(c^2 −ab))= (((x−y)(x+y+z))/((a−b)(a+b+c)))=(((y−z)(x+y+z))/((b−c)(a+b+c)))=(((z−x)(x+y+z))/((c−a)(a+b+c))) ⇒((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a))⇒...

$${Lemma}:\:\frac{{a}}{{b}}=\frac{{c}}{{d}}\Rightarrow\frac{{a}}{{b}}=\frac{{c}}{{d}}=\frac{{a}\underset{−} {+}{c}}{{b}\underset{−} {+}{d}} \\ $$$${Proof}:\:{Let}\:\frac{{a}}{{b}}=\frac{{c}}{{d}}={k}\Rightarrow{a}={bk}\:\wedge\:{c}={dk} \\ $$$$\Rightarrow{a}\underset{−} {+}{c}=\left({b}\underset{−} {+}{d}\right){k}\Rightarrow\frac{{a}\underset{−} {+}{c}}{{b}\underset{−} {+}{d}}={k}=\frac{{a}}{{c}}=\frac{{b}}{{d}}\:\Box \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} −{yz}}{{a}^{\mathrm{2}} −{bc}}=\frac{{y}^{\mathrm{2}} −{zx}}{{b}^{\mathrm{2}} −{ca}}=\frac{{z}^{\mathrm{2}} −{xy}}{{c}^{\mathrm{2}} −{ab}}= \\ $$$$\frac{\left({x}−{y}\right)\left({x}+{y}+{z}\right)}{\left({a}−{b}\right)\left({a}+{b}+{c}\right)}=\frac{\left({y}−{z}\right)\left({x}+{y}+{z}\right)}{\left({b}−{c}\right)\left({a}+{b}+{c}\right)}=\frac{\left({z}−{x}\right)\left({x}+{y}+{z}\right)}{\left({c}−{a}\right)\left({a}+{b}+{c}\right)} \\ $$$$\Rightarrow\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}}\Rightarrow... \\ $$

Commented by MATHEMATICSAM last updated on 18/Oct/24

I want to know that is there any process to get (x/a) = (y/b) = (z/c) from ((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a)) I want to reversely prove from ((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a)) to (x/a) = (y/b) = (z/c) By holding ((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a))=k or something

$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{that}\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{process} \\ $$$$\mathrm{to}\:\mathrm{get}\:\frac{{x}}{{a}}\:=\:\frac{{y}}{{b}}\:=\:\frac{{z}}{{c}}\:\mathrm{from}\: \\ $$$$\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}} \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{reversely}\:\mathrm{prove}\:\mathrm{from} \\ $$$$\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}}\:\mathrm{to}\:\frac{{x}}{{a}}\:=\:\frac{{y}}{{b}}\:=\:\frac{{z}}{{c}} \\ $$$$\mathrm{By}\:\mathrm{holding}\: \\ $$$$\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}}={k}\:\mathrm{or}\:\mathrm{something} \\ $$

Commented by A5T last updated on 18/Oct/24

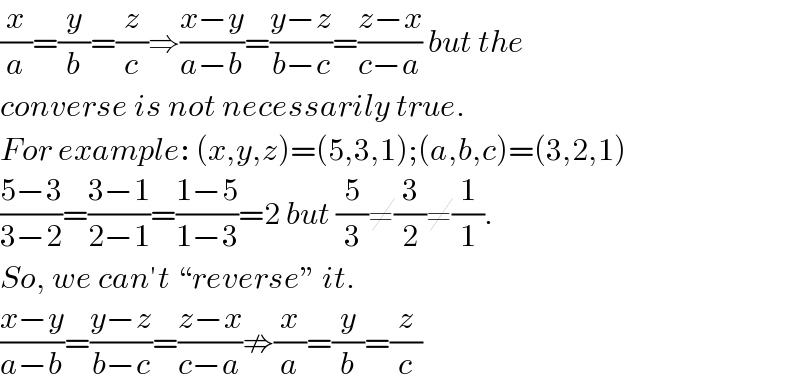
(x/a)=(y/b)=(z/c)⇒((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a)) but the converse is not necessarily true. For example: (x,y,z)=(5,3,1);(a,b,c)=(3,2,1) ((5−3)/(3−2))=((3−1)/(2−1))=((1−5)/(1−3))=2 but (5/3)≠(3/2)≠(1/1). So, we can′t “reverse” it. ((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a))⇏(x/a)=(y/b)=(z/c)

$$\frac{{x}}{{a}}=\frac{{y}}{{b}}=\frac{{z}}{{c}}\Rightarrow\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}}\:{but}\:{the}\: \\ $$$${converse}\:{is}\:{not}\:{necessarily}\:{true}. \\ $$$${For}\:{example}:\:\left({x},{y},{z}\right)=\left(\mathrm{5},\mathrm{3},\mathrm{1}\right);\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{1}\right) \\ $$$$\frac{\mathrm{5}−\mathrm{3}}{\mathrm{3}−\mathrm{2}}=\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}−\mathrm{1}}=\frac{\mathrm{1}−\mathrm{5}}{\mathrm{1}−\mathrm{3}}=\mathrm{2}\:{but}\:\frac{\mathrm{5}}{\mathrm{3}}\neq\frac{\mathrm{3}}{\mathrm{2}}\neq\frac{\mathrm{1}}{\mathrm{1}}. \\ $$$${So},\:{we}\:{can}'{t}\:``{reverse}''\:{it}. \\ $$$$\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}}\nRightarrow\frac{{x}}{{a}}=\frac{{y}}{{b}}=\frac{{z}}{{c}} \\ $$

Commented by Rasheed.Sindhi last updated on 19/Oct/24

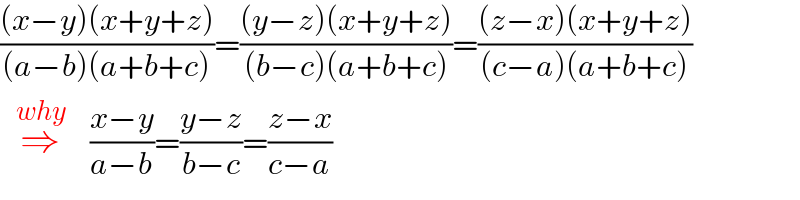
(((x−y)(x+y+z))/((a−b)(a+b+c)))=(((y−z)(x+y+z))/((b−c)(a+b+c)))=(((z−x)(x+y+z))/((c−a)(a+b+c))) ⇒^(why) ((x−y)/(a−b))=((y−z)/(b−c))=((z−x)/(c−a))

$$\frac{\left({x}−{y}\right)\left({x}+{y}+{z}\right)}{\left({a}−{b}\right)\left({a}+{b}+{c}\right)}=\frac{\left({y}−{z}\right)\left({x}+{y}+{z}\right)}{\left({b}−{c}\right)\left({a}+{b}+{c}\right)}=\frac{\left({z}−{x}\right)\left({x}+{y}+{z}\right)}{\left({c}−{a}\right)\left({a}+{b}+{c}\right)} \\ $$$$\:\:\overset{{why}} {\Rightarrow}\:\:\:\frac{{x}−{y}}{{a}−{b}}=\frac{{y}−{z}}{{b}−{c}}=\frac{{z}−{x}}{{c}−{a}} \\ $$

Commented by MATHEMATICSAM last updated on 19/Oct/24

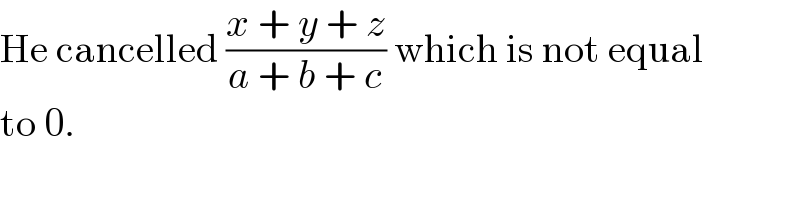
He cancelled ((x + y + z)/(a + b + c)) which is not equal to 0.

$$\mathrm{He}\:\mathrm{cancelled}\:\frac{{x}\:+\:{y}\:+\:{z}}{{a}\:+\:{b}\:+\:{c}}\:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{0}. \\ $$

Commented by Rasheed.Sindhi last updated on 19/Oct/24

Ok, thanks!

$${Ok},\:{thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com