Question and Answers Forum

All Questions      Topic List

Moderm Physics Questions

Previous in All Question      Next in All Question      

Previous in Moderm Physics      Next in Moderm Physics      

Question Number 158694 by ilhamdiii last updated on 07/Nov/21

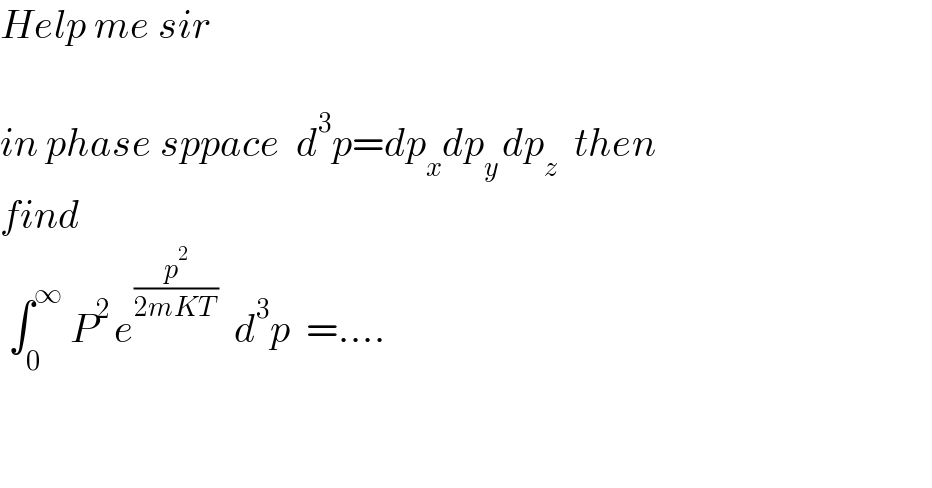
Help me sir in phase sppace d^3 p=dp_x dp_(y ) dp_z then find ∫_0 ^∞ P^(2 ) e^(p^2 /(2mKT )) d^3 p =....

$${Help}\:{me}\:{sir} \\ $$$$\: \\ $$$${in}\:{phase}\:{sppace}\:\:{d}^{\mathrm{3}} {p}={dp}_{{x}} {dp}_{{y}\:} {dp}_{{z}} \:\:{then} \\ $$$${find} \\ $$$$\:\int_{\mathrm{0}} ^{\infty} \:{P}^{\mathrm{2}\:} {e}^{\frac{{p}^{\mathrm{2}} }{\mathrm{2}{mKT}\:}} \:\:{d}^{\mathrm{3}} {p}\:\:=.... \\ $$$$ \\ $$$$ \\ $$

Answered by MrGaster last updated on 06/Jan/25

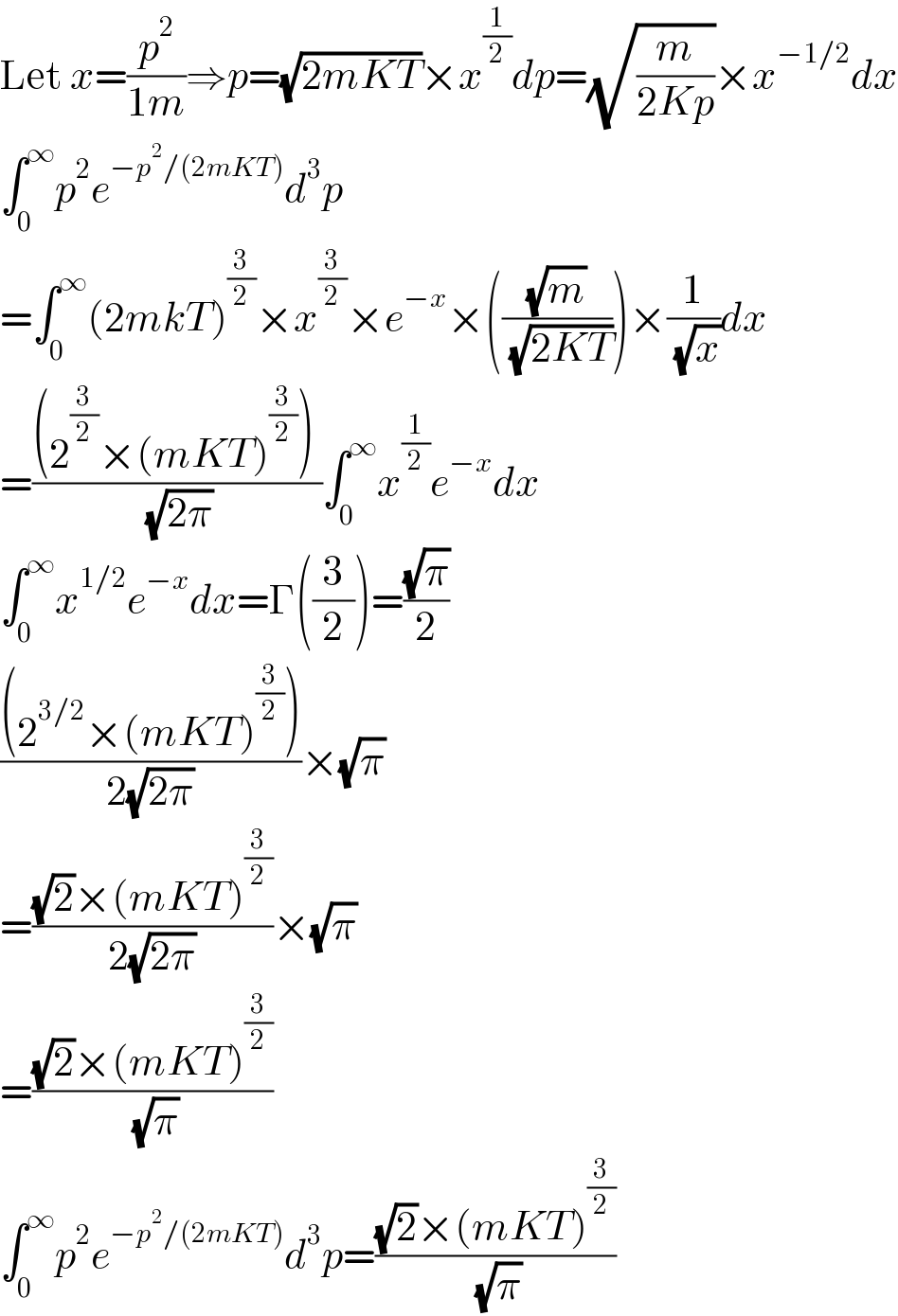
Let x=(p^2 /(1m))⇒p=(√(2mKT))×x^(1/2) dp=(√(m/(2Kp)))×x^(−1/2) dx ∫_0 ^∞ p^2 e^(−p^2 /(2mKT)) d^3 p =∫_0 ^∞ (2mkT)^(3/2) ×x^(3/2) ×e^(−x) ×(((√m)/( (√(2KT)))))×(1/( (√x)))dx =(((2^(3/2) ×(mKT)^(3/2) ) )/( (√(2π))))∫_0 ^∞ x^(1/2) e^(−x) dx ∫_0 ^∞ x^(1/2) e^(−x) dx=Γ((3/2))=((√π)/2) (((2^(3/2) ×(mKT)^(3/2) ))/(2(√(2π))))×(√π) =(((√2)×(mKT)^(3/2) )/(2(√(2π))))×(√π) =(((√2)×(mKT)^(3/2) )/( (√π))) ∫_0 ^∞ p^2 e^(−p^2 /(2mKT)) d^3 p=(((√2)×(mKT)^(3/2) )/( (√π)))

$$\mathrm{Let}\:{x}=\frac{{p}^{\mathrm{2}} }{\mathrm{1}{m}}\Rightarrow{p}=\sqrt{\mathrm{2}{mKT}}×{x}^{\frac{\mathrm{1}}{\mathrm{2}}} {dp}=\sqrt{\frac{{m}}{\mathrm{2}{Kp}}}×{x}^{−\mathrm{1}/\mathrm{2}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {p}^{\mathrm{2}} {e}^{−{p}^{\mathrm{2}} /\left(\mathrm{2}{mKT}\right)} {d}^{\mathrm{3}} {p} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{2}{mkT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{e}^{−{x}} ×\left(\frac{\sqrt{{m}}}{\:\sqrt{\mathrm{2}{KT}}}\right)×\frac{\mathrm{1}}{\:\sqrt{{x}}}{dx} \\ $$$$=\frac{\left(\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} ×\left({mKT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:}{\:\sqrt{\mathrm{2}\pi}}\int_{\mathrm{0}} ^{\infty} {x}^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{x}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}/\mathrm{2}} {e}^{−{x}} {dx}=\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{2}^{\mathrm{3}/\mathrm{2}} ×\left({mKT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right)}{\mathrm{2}\sqrt{\mathrm{2}\pi}}×\sqrt{\pi} \\ $$$$=\frac{\sqrt{\mathrm{2}}×\left({mKT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}\pi}}×\sqrt{\pi} \\ $$$$=\frac{\sqrt{\mathrm{2}}×\left({mKT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\:\sqrt{\pi}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {p}^{\mathrm{2}} {e}^{−{p}^{\mathrm{2}} /\left(\mathrm{2}{mKT}\right)} {d}^{\mathrm{3}} {p}=\frac{\sqrt{\mathrm{2}}×\left({mKT}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\:\sqrt{\pi}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com