
Question Number 67659 by Rio Michael last updated on 29/Aug/19

$${Help}\:{me}\:{obtain}\:\:\:{the}\:{value}\:{of}\:\:{e}\:{from} \\ $$$$\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{n}}\right)^{{n}} \:\:{how}\:{do}\:{i}\:{go}\:{about}\:{it}. \\ $$
Commented by Abdo msup. last updated on 30/Aug/19
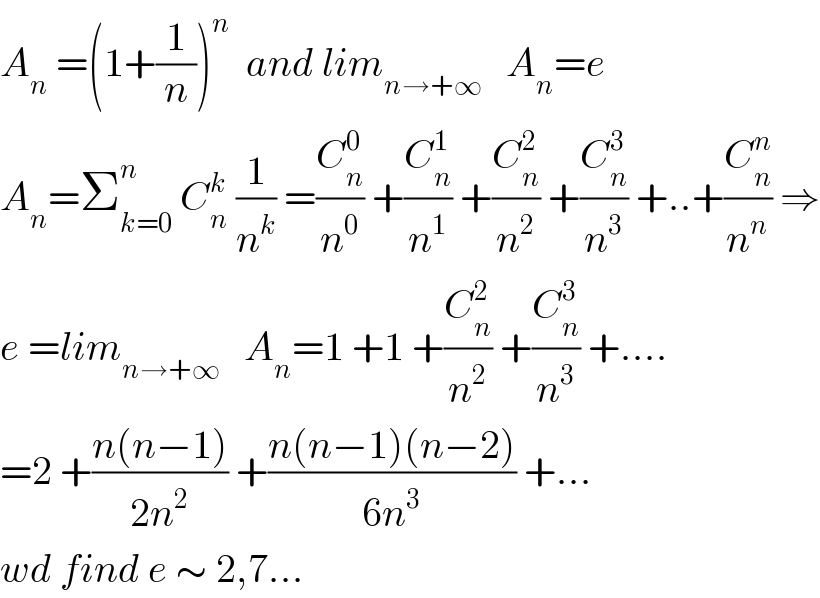
$${A}_{{n}} \:=\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:\:{and}\:{lim}_{{n}\rightarrow+\infty} \:\:\:{A}_{{n}} ={e} \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\frac{\mathrm{1}}{{n}^{{k}} }\:=\frac{{C}_{{n}} ^{\mathrm{0}} }{{n}^{\mathrm{0}} }\:+\frac{{C}_{{n}} ^{\mathrm{1}} }{{n}^{\mathrm{1}} }\:+\frac{{C}_{{n}} ^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:+\frac{{C}_{{n}} ^{\mathrm{3}} }{{n}^{\mathrm{3}} }\:+..+\frac{{C}_{{n}} ^{{n}} }{{n}^{{n}} }\:\Rightarrow \\ $$$${e}\:={lim}_{{n}\rightarrow+\infty} \:\:\:{A}_{{n}} =\mathrm{1}\:+\mathrm{1}\:+\frac{{C}_{{n}} ^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:+\frac{{C}_{{n}} ^{\mathrm{3}} }{{n}^{\mathrm{3}} }\:+.... \\ $$$$=\mathrm{2}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{6}{n}^{\mathrm{3}} }\:+... \\ $$$${wd}\:{find}\:{e}\:\sim\:\mathrm{2},\mathrm{7}... \\ $$
Commented by Rio Michael last updated on 30/Aug/19

$${thanks}\:{sir} \\ $$
Commented by Abdo msup. last updated on 30/Aug/19
$${you}\:{are}\:{welcome}. \\ $$
