
Question Number 203321 by SonGoku last updated on 16/Jan/24

$$\mathrm{Help}-\mathrm{me}! \\ $$$$\: \\ $$$$\mathrm{Observe}\:\mathrm{points}\:\mathrm{A},\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{below}\:\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{widthof}\:\mathrm{a}\:\mathrm{lake}\:\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{following}\:\mathrm{data}: \\ $$$$\: \\ $$$$\left(\mathrm{AB}\right)\mathrm{m};\:\hat {\mathrm{C}}\:=\:\mathrm{39}°\mathrm{52}'\mathrm{12}'' \\ $$$$\left(\mathrm{BC}\:−\:\mathrm{257}.\mathrm{5}\right)\mathrm{m};\:\hat {\mathrm{A}}\:=\:\mathrm{97}°\mathrm{7}'\mathrm{56}'' \\ $$$$\left(\mathrm{CA}\:−\:\mathrm{30}\right)\mathrm{m};\:\hat {\mathrm{B}}\:=\:\mathrm{42}°\mathrm{59}'\mathrm{52}'' \\ $$$$\mathrm{CA}\:\mathrm{is}\:\mathrm{the}\:\mathrm{width}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lake}\: \\ $$$$\: \\ $$$$\bullet^{\mathrm{C}} \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\bullet_{\mathrm{A}} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bullet_{\mathrm{B}} \\ $$
Answered by esmaeil last updated on 17/Jan/24
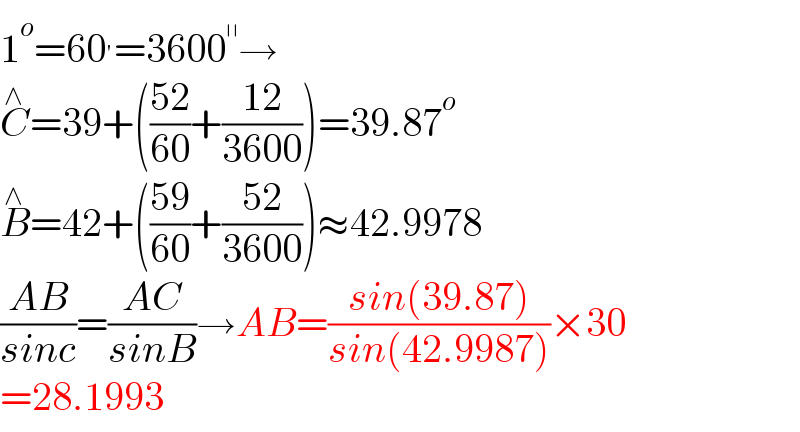
$$\mathrm{1}^{{o}} =\mathrm{60}^{'} =\mathrm{3600}^{\shortparallel} \rightarrow \\ $$$$\overset{\wedge} {{C}}=\mathrm{39}+\left(\frac{\mathrm{52}}{\mathrm{60}}+\frac{\mathrm{12}}{\mathrm{3600}}\right)=\mathrm{39}.\mathrm{87}^{{o}} \\ $$$$\overset{\wedge} {{B}}=\mathrm{42}+\left(\frac{\mathrm{59}}{\mathrm{60}}+\frac{\mathrm{52}}{\mathrm{3600}}\right)\approx\mathrm{42}.\mathrm{9978} \\ $$$$\frac{{AB}}{{sinc}}=\frac{{AC}}{{sinB}}\rightarrow{AB}=\frac{{sin}\left(\mathrm{39}.\mathrm{87}\right)}{{sin}\left(\mathrm{42}.\mathrm{9987}\right)}×\mathrm{30} \\ $$$$=\mathrm{28}.\mathrm{1993} \\ $$
