Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 194176 by Skabetix last updated on 29/Jun/23

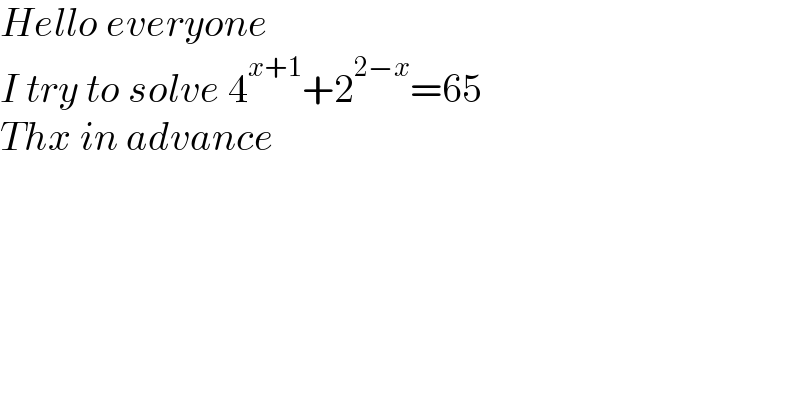
Hello everyone I try to solve 4^(x+1) +2^(2−x) =65 Thx in advance

$${Hello}\:{everyone} \\ $$$${I}\:{try}\:{to}\:{solve}\:\mathrm{4}^{{x}+\mathrm{1}} +\mathrm{2}^{\mathrm{2}−{x}} =\mathrm{65} \\ $$$${Thx}\:{in}\:{advance} \\ $$

Answered by Skabetix last updated on 29/Jun/23

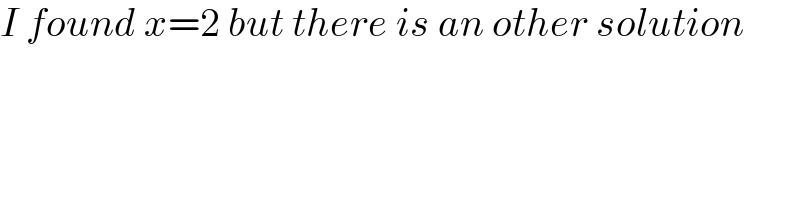
I found x=2 but there is an other solution

$${I}\:{found}\:{x}=\mathrm{2}\:{but}\:{there}\:{is}\:{an}\:{other}\:{solution} \\ $$

Answered by mr W last updated on 29/Jun/23

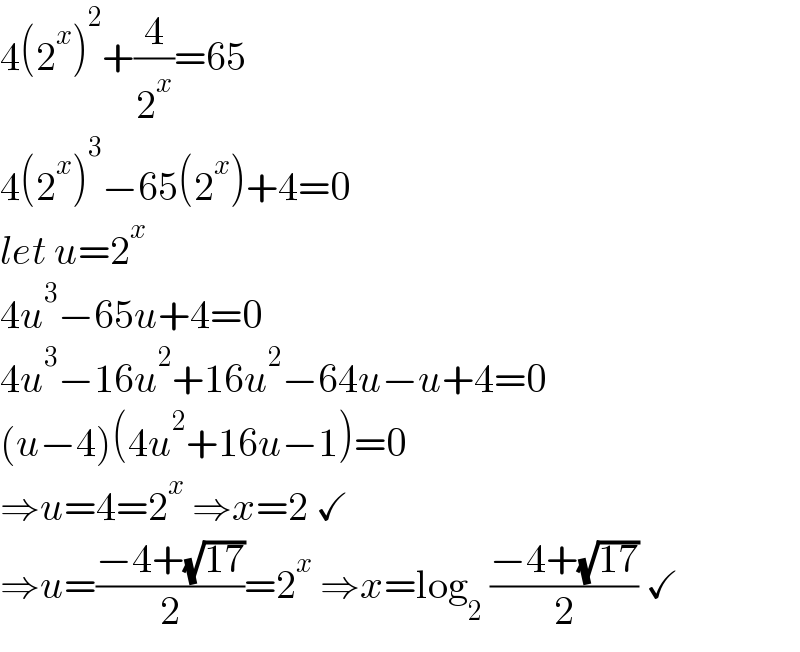
4(2^x )^2 +(4/2^x )=65 4(2^x )^3 −65(2^x )+4=0 let u=2^x 4u^3 −65u+4=0 4u^3 −16u^2 +16u^2 −64u−u+4=0 (u−4)(4u^2 +16u−1)=0 ⇒u=4=2^x ⇒x=2 ✓ ⇒u=((−4+(√(17)))/2)=2^x ⇒x=log_2 ((−4+(√(17)))/2) ✓

$$\mathrm{4}\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{2}^{{x}} }=\mathrm{65} \\ $$$$\mathrm{4}\left(\mathrm{2}^{{x}} \right)^{\mathrm{3}} −\mathrm{65}\left(\mathrm{2}^{{x}} \right)+\mathrm{4}=\mathrm{0} \\ $$$${let}\:{u}=\mathrm{2}^{{x}} \\ $$$$\mathrm{4}{u}^{\mathrm{3}} −\mathrm{65}{u}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}{u}^{\mathrm{3}} −\mathrm{16}{u}^{\mathrm{2}} +\mathrm{16}{u}^{\mathrm{2}} −\mathrm{64}{u}−{u}+\mathrm{4}=\mathrm{0} \\ $$$$\left({u}−\mathrm{4}\right)\left(\mathrm{4}{u}^{\mathrm{2}} +\mathrm{16}{u}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{u}=\mathrm{4}=\mathrm{2}^{{x}} \:\Rightarrow{x}=\mathrm{2}\:\checkmark \\ $$$$\Rightarrow{u}=\frac{−\mathrm{4}+\sqrt{\mathrm{17}}}{\mathrm{2}}=\mathrm{2}^{{x}} \:\Rightarrow{x}=\mathrm{log}_{\mathrm{2}} \:\frac{−\mathrm{4}+\sqrt{\mathrm{17}}}{\mathrm{2}}\:\checkmark \\ $$

Answered by MM42 last updated on 29/Jun/23

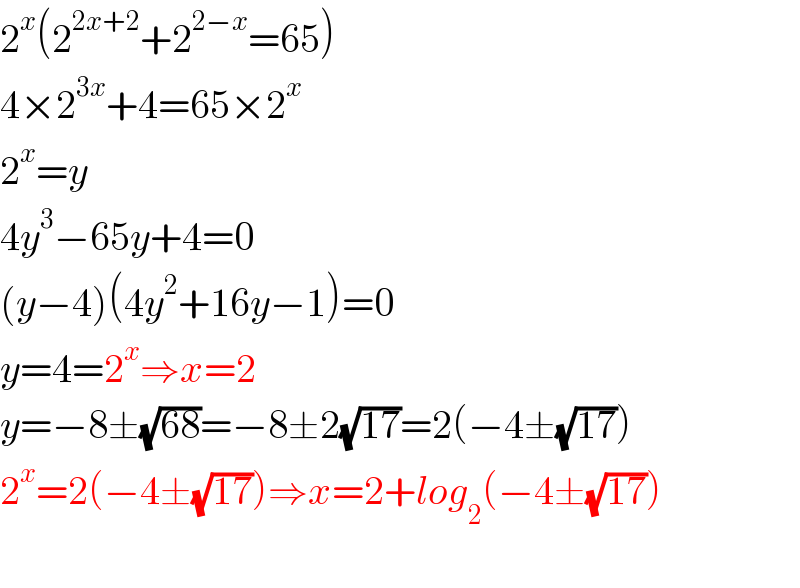
2^x (2^(2x+2) +2^(2−x) =65) 4×2^(3x) +4=65×2^x 2^x =y 4y^3 −65y+4=0 (y−4)(4y^2 +16y−1)=0 y=4=2^x ⇒x=2 y=−8±(√(68))=−8±2(√(17))=2(−4±(√(17))) 2^x =2(−4±(√(17)))⇒x=2+log_2 (−4±(√(17)))

$$\mathrm{2}^{{x}} \left(\mathrm{2}^{\mathrm{2}{x}+\mathrm{2}} +\mathrm{2}^{\mathrm{2}−{x}} =\mathrm{65}\right) \\ $$$$\mathrm{4}×\mathrm{2}^{\mathrm{3}{x}} +\mathrm{4}=\mathrm{65}×\mathrm{2}^{{x}} \\ $$$$\mathrm{2}^{{x}} ={y} \\ $$$$\mathrm{4}{y}^{\mathrm{3}} −\mathrm{65}{y}+\mathrm{4}=\mathrm{0} \\ $$$$\left({y}−\mathrm{4}\right)\left(\mathrm{4}{y}^{\mathrm{2}} +\mathrm{16}{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}=\mathrm{4}=\mathrm{2}^{{x}} \Rightarrow{x}=\mathrm{2} \\ $$$${y}=−\mathrm{8}\pm\sqrt{\mathrm{68}}=−\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{17}}=\mathrm{2}\left(−\mathrm{4}\pm\sqrt{\mathrm{17}}\right) \\ $$$$\mathrm{2}^{{x}} =\mathrm{2}\left(−\mathrm{4}\pm\sqrt{\mathrm{17}}\right)\Rightarrow{x}=\mathrm{2}+{log}_{\mathrm{2}} \left(−\mathrm{4}\pm\sqrt{\mathrm{17}}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com