
Question Number 209021 by hardmath last updated on 30/Jun/24

$$ \\ $$Hello, I present to you an interesting combinatorics question: A group of people from k families should be seated around a round table, with a_{i} number of people in the i family. Each family member must sit together (i.e. no family member can sit between other family members). There are l spaces around the table. There are seats (l>k). How many ways can we seat k number of families around a round table under these conditions.
Commented by mr W last updated on 30/Jun/24

$${can}\:{you}\:{please}\:{read}\:{your}\:{question}\: \\ $$$${carefully}\:{once}\:{again}\:{and}\:{check}\:{if} \\ $$$${some}\:{data}\:{are}\:{missing}\:{or}\:{wrong}\:{or} \\ $$$${unclear}? \\ $$
Commented by mr W last updated on 30/Jun/24

$${clear}: \\ $$$${there}\:{are}\:{k}\:{families}.\:{the}\:{family}\:{i} \\ $$$${has}\:{a}_{{i}} \:{members}\:\left({with}\:{i}=\mathrm{1},\mathrm{2},\:...,\:{k}\right). \\ $$$${the}\:{members}\:{of}\:{each}\:{family}\:{must} \\ $$$${sit}\:{together}. \\ $$$${unclear}: \\ $$$${there}\:{are}\:{I}\:{spaces}\:{around}\:{the}\:{table}. \\ $$$${what}\:{do}\:{you}\:{mean}\:{with}\:``{spaces}''? \\ $$$${there}\:{are}\:{seats}\:\left({I}>{k}\right). \\ $$$${is}\:{something}\:{missing}? \\ $$$${do}\:{you}\:{want}\:{to}\:{say}\:{a}\:{speical}\:{number} \\ $$$${of}\:{seats}? \\ $$$${how}\:{many}\:{ways}\:{can}\:{we}\:{seat}\:{k} \\ $$$${member}\:{of}\:{families}\:{around}\:{a}\:{round} \\ $$$${table}. \\ $$$${do}\:{you}\:{mean}\:{all}\:{the}\:{members}\:{of}\:{k} \\ $$$${families}? \\ $$
Commented by hardmath last updated on 30/Jun/24

$$\mathrm{Dear}\:\mathrm{Professor}, \\ $$$$ \\ $$Yes, we have L empty seats around the table (which people should sit on those seats), the question is how to seat all the people around the table under these conditions (if you see, the number of people is a_1+a_2+..+a_k)
Commented by mr W last updated on 30/Jun/24
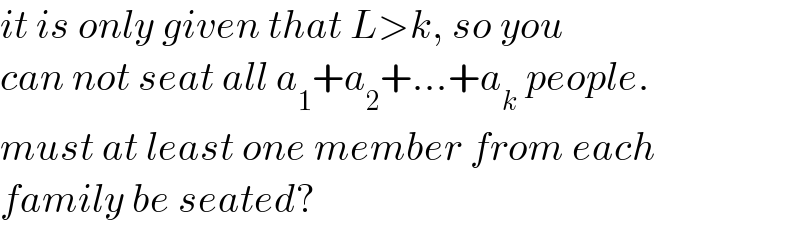
$${it}\:{is}\:{only}\:{given}\:{that}\:{L}>{k},\:{so}\:{you} \\ $$$${can}\:{not}\:{seat}\:{all}\:{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{{k}} \:{people}. \\ $$$${must}\:{at}\:{least}\:{one}\:{member}\:{from}\:{each} \\ $$$${family}\:{be}\:{seated}? \\ $$
Commented by hardmath last updated on 30/Jun/24

$$\mathrm{Dear}\:\mathrm{Professor},\:\mathrm{sorry} \\ $$$$ \\ $$It is true that there was a mistake in the l>k part, that is, l > a1+a2+...+ak is given, that is, we have enough seats.
Commented by mr W last updated on 30/Jun/24
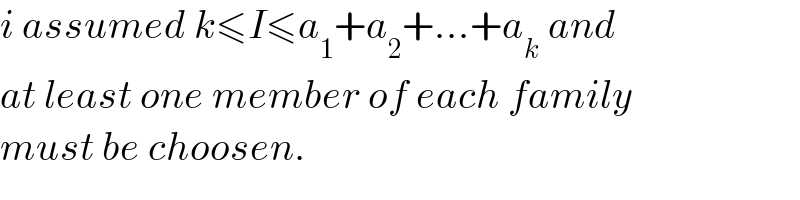
$${i}\:{assumed}\:{k}\leqslant{I}\leqslant{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{{k}} \:{and} \\ $$$${at}\:{least}\:{one}\:{member}\:{of}\:{each}\:{family} \\ $$$${must}\:{be}\:{choosen}. \\ $$
Commented by hardmath last updated on 30/Jun/24

$$ \\ $$
Answered by mr W last updated on 30/Jun/24
![I seats around a round table are to be taken by the members of k families and the members of the same family must sit together. that means at least one member of each family must be choosen. to arrange k families around the round table there are (k−1)! ways. say from family i we choose n_i members, 1≤n_i ≤a_i . n_1 +n_2 +n_3 +...+n_k =I with I ≥k to select n_i from a_i members in the family i there are C_n_i ^a_i ways and to arrange them there are n_i ! ways. so the total number of ways is the coefficient of term x^I in the expansion (k−1)!Π_(i=1) ^k [Σ_(n_i =1) ^a_i C_n_i ^a_i (n_i !)x^n_i ]](Q209045.png)
$${I}\:{seats}\:{around}\:{a}\:{round}\:{table}\:{are}\:{to} \\ $$$${be}\:{taken}\:{by}\:{the}\:{members}\:{of}\:{k}\: \\ $$$${families}\:{and}\:{the}\:{members}\:{of}\:{the} \\ $$$${same}\:{family}\:{must}\:{sit}\:{together}. \\ $$$${that}\:{means}\:{at}\:{least}\:{one}\:{member}\:{of} \\ $$$${each}\:{family}\:{must}\:{be}\:{choosen}. \\ $$$${to}\:{arrange}\:{k}\:{families}\:{around}\:{the} \\ $$$${round}\:{table}\:{there}\:{are}\:\left({k}−\mathrm{1}\right)!\:{ways}. \\ $$$${say}\:{from}\:{family}\:{i}\:{we}\:{choose}\:{n}_{{i}} \: \\ $$$${members},\:\mathrm{1}\leqslant{n}_{{i}} \leqslant{a}_{{i}} . \\ $$$${n}_{\mathrm{1}} +{n}_{\mathrm{2}} +{n}_{\mathrm{3}} +...+{n}_{{k}} ={I}\:\:\:{with}\:{I}\:\geqslant{k} \\ $$$${to}\:{select}\:{n}_{{i}} \:{from}\:{a}_{{i}} \:{members}\:{in}\:{the} \\ $$$${family}\:{i}\:{there}\:{are}\:{C}_{{n}_{{i}} } ^{{a}_{{i}} } \:{ways}\:{and}\:{to} \\ $$$${arrange}\:{them}\:{there}\:{are}\:{n}_{{i}} !\:{ways}. \\ $$$${so}\:{the}\:{total}\:{number}\:{of}\:{ways}\:{is}\:{the} \\ $$$${coefficient}\:{of}\:{term}\:{x}^{{I}} \:{in}\:{the}\: \\ $$$${expansion} \\ $$$$\left({k}−\mathrm{1}\right)!\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left[\underset{{n}_{{i}} =\mathrm{1}} {\overset{{a}_{{i}} } {\sum}}{C}_{{n}_{{i}} } ^{{a}_{{i}} } \left({n}_{{i}} !\right){x}^{{n}_{{i}} } \right] \\ $$
Commented by hardmath last updated on 30/Jun/24

$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}... \\ $$$$ \\ $$That is, the final result is our answer given in red.?
Commented by mr W last updated on 30/Jun/24

$${it}\:{is}\:{just}\:{a}\:{generating}\:{function}.\:{its} \\ $$$${coefficient}\:{of}\:{x}^{{I}} \:{term}\:{is}\:{the}\:{answer}. \\ $$$${but}\:{we}\:{can}\:{not}\:{get}\:{a}\:{closed}\:{formula} \\ $$$${for}\:{the}\:{answer}. \\ $$
Commented by mr W last updated on 30/Jun/24
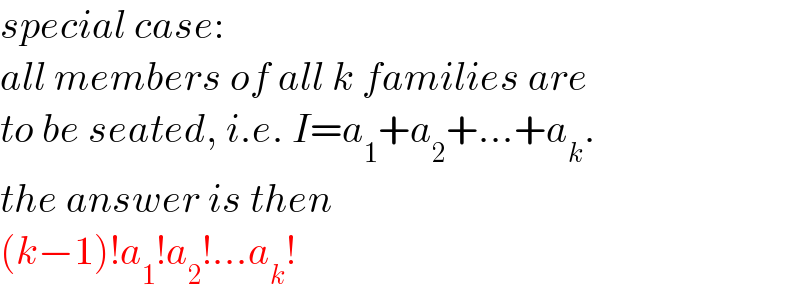
$${special}\:{case}: \\ $$$${all}\:{members}\:{of}\:{all}\:{k}\:{families}\:{are} \\ $$$${to}\:{be}\:{seated},\:{i}.{e}.\:{I}={a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{{k}} . \\ $$$${the}\:{answer}\:{is}\:{then} \\ $$$$\left({k}−\mathrm{1}\right)!{a}_{\mathrm{1}} !{a}_{\mathrm{2}} !...{a}_{{k}} ! \\ $$
Commented by hardmath last updated on 30/Jun/24

$$ \\ $$Thank you very much dear Peafessor for the detailed explanation, I mentioned the full version of the question above on the page
Commented by mr W last updated on 01/Jul/24
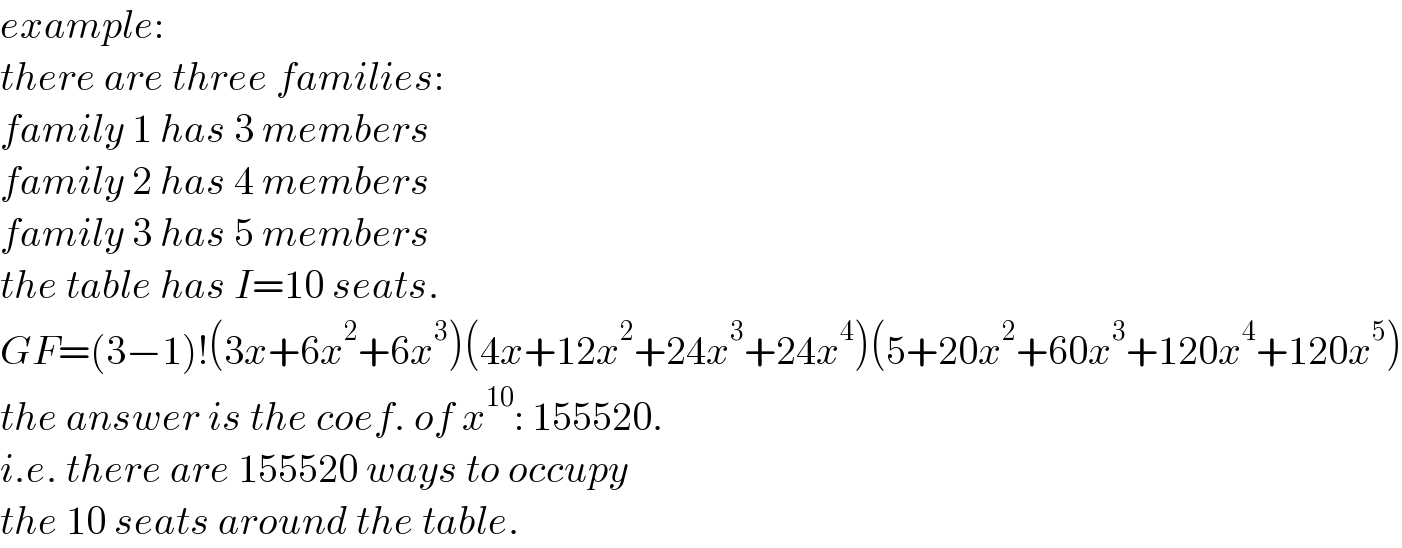
$${example}: \\ $$$${there}\:{are}\:{three}\:{families}: \\ $$$${family}\:\mathrm{1}\:{has}\:\mathrm{3}\:{members} \\ $$$${family}\:\mathrm{2}\:{has}\:\mathrm{4}\:{members} \\ $$$${family}\:\mathrm{3}\:{has}\:\mathrm{5}\:{members} \\ $$$${the}\:{table}\:{has}\:{I}=\mathrm{10}\:{seats}. \\ $$$${GF}=\left(\mathrm{3}−\mathrm{1}\right)!\left(\mathrm{3}{x}+\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{3}} \right)\left(\mathrm{4}{x}+\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}{x}^{\mathrm{3}} +\mathrm{24}{x}^{\mathrm{4}} \right)\left(\mathrm{5}+\mathrm{20}{x}^{\mathrm{2}} +\mathrm{60}{x}^{\mathrm{3}} +\mathrm{120}{x}^{\mathrm{4}} +\mathrm{120}{x}^{\mathrm{5}} \right) \\ $$$${the}\:{answer}\:{is}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{10}} :\:\mathrm{155520}. \\ $$$${i}.{e}.\:{there}\:{are}\:\mathrm{155520}\:{ways}\:{to}\:{occupy} \\ $$$${the}\:\mathrm{10}\:{seats}\:{around}\:{the}\:{table}. \\ $$
Commented by mr W last updated on 01/Jul/24

