Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 218400 by SdC355 last updated on 09/Apr/25

Hard problem..... prove. for all α∈Z α^(37) ≡α Mod(1729) pls help :(

$$\mathrm{Hard}\:\mathrm{problem}..... \\ $$$$\:\mathrm{prove}. \\ $$$$\:\mathrm{for}\:\mathrm{all}\:\alpha\in\mathbb{Z} \\ $$$$\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{Mod}\left(\mathrm{1729}\right) \\ $$$$\mathrm{pls}\:\mathrm{help}\::\left(\right. \\ $$

Answered by Nicholas666 last updated on 09/Apr/25

$$ \\ $$

Answered by Nicholas666 last updated on 09/Apr/25

$$ \\ $$

Answered by vnm last updated on 09/Apr/25

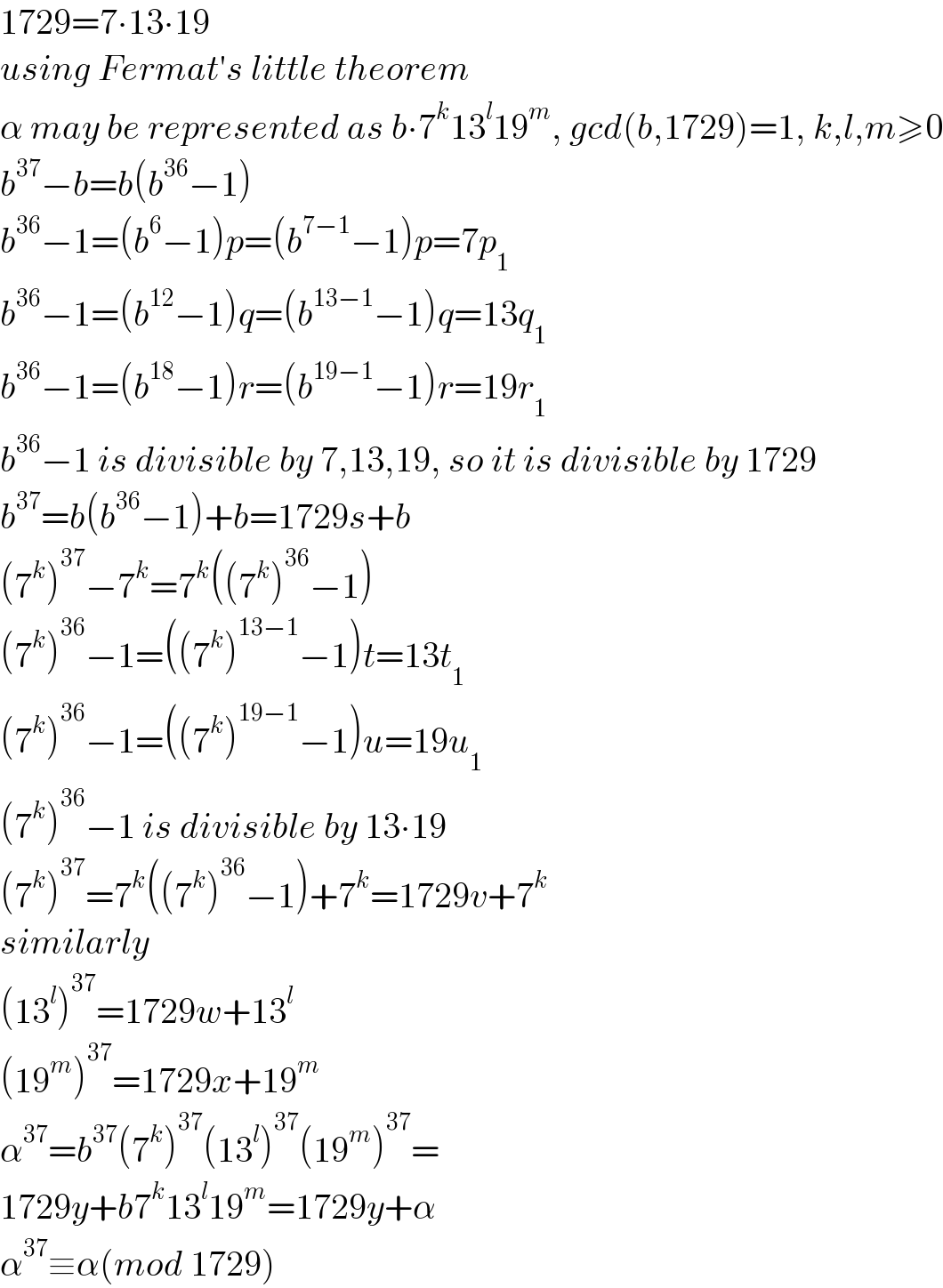
1729=7∙13∙19 using Fermat′s little theorem α may be represented as b∙7^k 13^l 19^m , gcd(b,1729)=1, k,l,m≥0 b^(37) −b=b(b^(36) −1) b^(36) −1=(b^6 −1)p=(b^(7−1) −1)p=7p_1 b^(36) −1=(b^(12) −1)q=(b^(13−1) −1)q=13q_1 b^(36) −1=(b^(18) −1)r=(b^(19−1) −1)r=19r_1 b^(36) −1 is divisible by 7,13,19, so it is divisible by 1729 b^(37) =b(b^(36) −1)+b=1729s+b (7^k )^(37) −7^k =7^k ((7^k )^(36) −1) (7^k )^(36) −1=((7^k )^(13−1) −1)t=13t_1 (7^k )^(36) −1=((7^k )^(19−1) −1)u=19u_1 (7^k )^(36) −1 is divisible by 13∙19 (7^k )^(37) =7^k ((7^k )^(36) −1)+7^k =1729v+7^k similarly (13^l )^(37) =1729w+13^l (19^m )^(37) =1729x+19^m α^(37) =b^(37) (7^k )^(37) (13^l )^(37) (19^m )^(37) = 1729y+b7^k 13^l 19^m =1729y+α α^(37) ≡α(mod 1729)

$$\mathrm{1729}=\mathrm{7}\centerdot\mathrm{13}\centerdot\mathrm{19} \\ $$$${using}\:{Fermat}'{s}\:{little}\:{theorem} \\ $$$$\alpha\:{may}\:{be}\:{represented}\:{as}\:{b}\centerdot\mathrm{7}^{{k}} \mathrm{13}^{{l}} \mathrm{19}^{{m}} ,\:{gcd}\left({b},\mathrm{1729}\right)=\mathrm{1},\:{k},{l},{m}\geqslant\mathrm{0} \\ $$$${b}^{\mathrm{37}} −{b}={b}\left({b}^{\mathrm{36}} −\mathrm{1}\right) \\ $$$${b}^{\mathrm{36}} −\mathrm{1}=\left({b}^{\mathrm{6}} −\mathrm{1}\right){p}=\left({b}^{\mathrm{7}−\mathrm{1}} −\mathrm{1}\right){p}=\mathrm{7}{p}_{\mathrm{1}} \\ $$$${b}^{\mathrm{36}} −\mathrm{1}=\left({b}^{\mathrm{12}} −\mathrm{1}\right){q}=\left({b}^{\mathrm{13}−\mathrm{1}} −\mathrm{1}\right){q}=\mathrm{13}{q}_{\mathrm{1}} \\ $$$${b}^{\mathrm{36}} −\mathrm{1}=\left({b}^{\mathrm{18}} −\mathrm{1}\right){r}=\left({b}^{\mathrm{19}−\mathrm{1}} −\mathrm{1}\right){r}=\mathrm{19}{r}_{\mathrm{1}} \\ $$$${b}^{\mathrm{36}} −\mathrm{1}\:{is}\:{divisible}\:{by}\:\mathrm{7},\mathrm{13},\mathrm{19},\:{so}\:{it}\:{is}\:{divisible}\:{by}\:\mathrm{1729} \\ $$$${b}^{\mathrm{37}} ={b}\left({b}^{\mathrm{36}} −\mathrm{1}\right)+{b}=\mathrm{1729}{s}+{b} \\ $$$$\left(\mathrm{7}^{{k}} \right)^{\mathrm{37}} −\mathrm{7}^{{k}} =\mathrm{7}^{{k}} \left(\left(\mathrm{7}^{{k}} \right)^{\mathrm{36}} −\mathrm{1}\right) \\ $$$$\left(\mathrm{7}^{{k}} \right)^{\mathrm{36}} −\mathrm{1}=\left(\left(\mathrm{7}^{{k}} \right)^{\mathrm{13}−\mathrm{1}} −\mathrm{1}\right){t}=\mathrm{13}{t}_{\mathrm{1}} \\ $$$$\left(\mathrm{7}^{{k}} \right)^{\mathrm{36}} −\mathrm{1}=\left(\left(\mathrm{7}^{{k}} \right)^{\mathrm{19}−\mathrm{1}} −\mathrm{1}\right){u}=\mathrm{19}{u}_{\mathrm{1}} \\ $$$$\left(\mathrm{7}^{{k}} \right)^{\mathrm{36}} −\mathrm{1}\:{is}\:{divisible}\:{by}\:\mathrm{13}\centerdot\mathrm{19} \\ $$$$\left(\mathrm{7}^{{k}} \right)^{\mathrm{37}} =\mathrm{7}^{{k}} \left(\left(\mathrm{7}^{{k}} \right)^{\mathrm{36}} −\mathrm{1}\right)+\mathrm{7}^{{k}} =\mathrm{1729}{v}+\mathrm{7}^{{k}} \\ $$$${similarly} \\ $$$$\left(\mathrm{13}^{{l}} \right)^{\mathrm{37}} =\mathrm{1729}{w}+\mathrm{13}^{{l}} \\ $$$$\left(\mathrm{19}^{{m}} \right)^{\mathrm{37}} =\mathrm{1729}{x}+\mathrm{19}^{{m}} \\ $$$$\alpha^{\mathrm{37}} ={b}^{\mathrm{37}} \left(\mathrm{7}^{{k}} \right)^{\mathrm{37}} \left(\mathrm{13}^{{l}} \right)^{\mathrm{37}} \left(\mathrm{19}^{{m}} \right)^{\mathrm{37}} = \\ $$$$\mathrm{1729}{y}+{b}\mathrm{7}^{{k}} \mathrm{13}^{{l}} \mathrm{19}^{{m}} =\mathrm{1729}{y}+\alpha \\ $$$$\alpha^{\mathrm{37}} \equiv\alpha\left({mod}\:\mathrm{1729}\right) \\ $$

Answered by MrGaster last updated on 10/Apr/25

Z∈α=α mod 1729⇒α^(37) ≡α mod 7 ∩ α^(37) ≡α mod 13∩ α^(37) =α mod 19 1729=7×13×19(Prime factorization) ∀p∈{7,13,19},α^(p−1) ≡1 mod p⇒α^(37) ≡α^(37 mod ( p−1)) mod p 37≡1 mod 6⇒α^(37) ≡α mod 7 37≡1 mod 12⇒α^(37) ≡α mod 13 37≡1 mod 18⇒α^(37) ≡α mod 19 α^(37) ≡α mod 7∩α^(37) ≡α mod 13 ∩α^(37) =α mod 19⇒α^(37) ≡α mod lcm(7,13,19) lcm(7,13,19)=7×13×19=1729⇒α^(37) ≡α Mod(1729)

$$\mathbb{Z}\in\alpha=\alpha\:\mathrm{mod}\:\mathrm{1729}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{7}\:\cap\:\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{13}\cap\:\alpha^{\mathrm{37}} =\alpha\:\mathrm{mod}\:\mathrm{19} \\ $$$$\mathrm{1729}=\mathrm{7}×\mathrm{13}×\mathrm{19}\left(\mathrm{Prime}\:\mathrm{factorization}\right) \\ $$$$\forall{p}\in\left\{\mathrm{7},\mathrm{13},\mathrm{19}\right\},\alpha^{{p}−\mathrm{1}} \equiv\mathrm{1}\:\mathrm{mod}\:{p}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha^{\mathrm{37}\:\mathrm{mod}\:\left(\:{p}−\mathrm{1}\right)} \mathrm{mod}\:{p} \\ $$$$\mathrm{37}\equiv\mathrm{1}\:\mathrm{mod}\:\mathrm{6}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{7} \\ $$$$\mathrm{37}\equiv\mathrm{1}\:\mathrm{mod}\:\mathrm{12}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{13} \\ $$$$\mathrm{37}\equiv\mathrm{1}\:\mathrm{mod}\:\mathrm{18}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{19} \\ $$$$\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{7}\cap\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{13}\:\cap\alpha^{\mathrm{37}} =\alpha\:\mathrm{mod}\:\mathrm{19}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{mod}\:\mathrm{lcm}\left(\mathrm{7},\mathrm{13},\mathrm{19}\right) \\ $$$$\mathrm{lcm}\left(\mathrm{7},\mathrm{13},\mathrm{19}\right)=\mathrm{7}×\mathrm{13}×\mathrm{19}=\mathrm{1729}\Rightarrow\alpha^{\mathrm{37}} \equiv\alpha\:\mathrm{Mod}\left(\mathrm{1729}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com