
Previous in Relation and Functions Next in Relation and Functions
Question Number 162823 by john_santu last updated on 01/Jan/22

$$\:\:{Given}:\:\:{x}.{p}\left({x}−\mathrm{1}\right)=\left({x}−\mathrm{5}\right).{p}\left({x}\right) \\ $$$$\:\:{and}\:{p}\left(−\mathrm{1}\right)=\mathrm{1}.\: \\ $$$$\:\:{Find}\:{p}\left(\frac{\mathrm{1}}{\mathrm{2}}\right). \\ $$
Answered by mr W last updated on 02/Jan/22
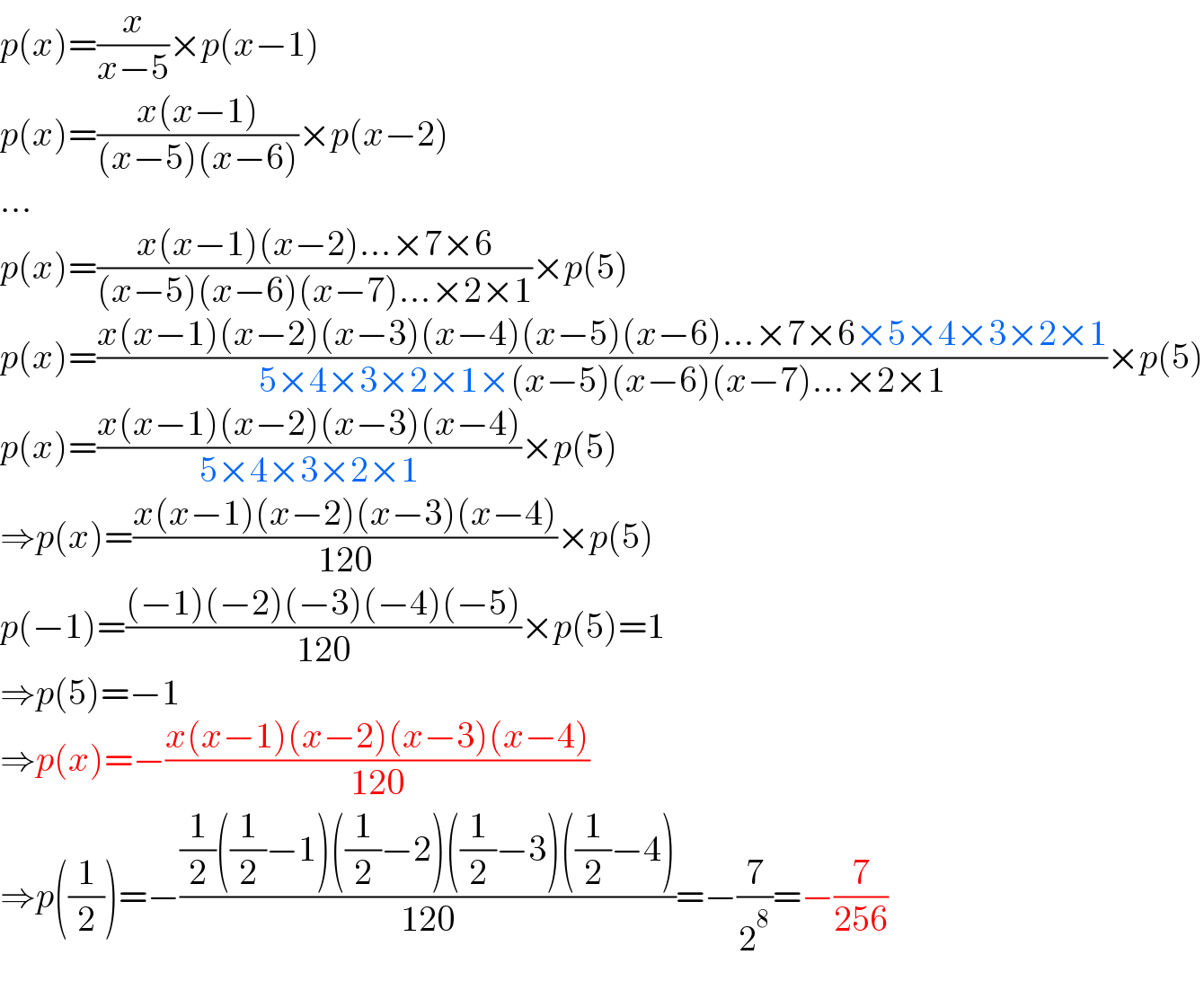
$${p}\left({x}\right)=\frac{{x}}{{x}−\mathrm{5}}×{p}\left({x}−\mathrm{1}\right) \\ $$$${p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)}{\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)}×{p}\left({x}−\mathrm{2}\right) \\ $$$$... \\ $$$${p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)...×\mathrm{7}×\mathrm{6}}{\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)...×\mathrm{2}×\mathrm{1}}×{p}\left(\mathrm{5}\right) \\ $$$${p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)...×\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}×\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)...×\mathrm{2}×\mathrm{1}}×{p}\left(\mathrm{5}\right) \\ $$$${p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}×{p}\left(\mathrm{5}\right) \\ $$$$\Rightarrow{p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}{\mathrm{120}}×{p}\left(\mathrm{5}\right) \\ $$$${p}\left(−\mathrm{1}\right)=\frac{\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)\left(−\mathrm{5}\right)}{\mathrm{120}}×{p}\left(\mathrm{5}\right)=\mathrm{1} \\ $$$$\Rightarrow{p}\left(\mathrm{5}\right)=−\mathrm{1} \\ $$$$\Rightarrow{p}\left({x}\right)=−\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}{\mathrm{120}} \\ $$$$\Rightarrow{p}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{3}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4}\right)}{\mathrm{120}}=−\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{8}} }=−\frac{\mathrm{7}}{\mathrm{256}} \\ $$
Commented by Tawa11 last updated on 02/Jan/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 02/Jan/22

$$\mathcal{X}{cellent}\:\mathcal{S}{ir}! \\ $$🏆🏅🎖️🥇
Answered by Rasheed.Sindhi last updated on 02/Jan/22
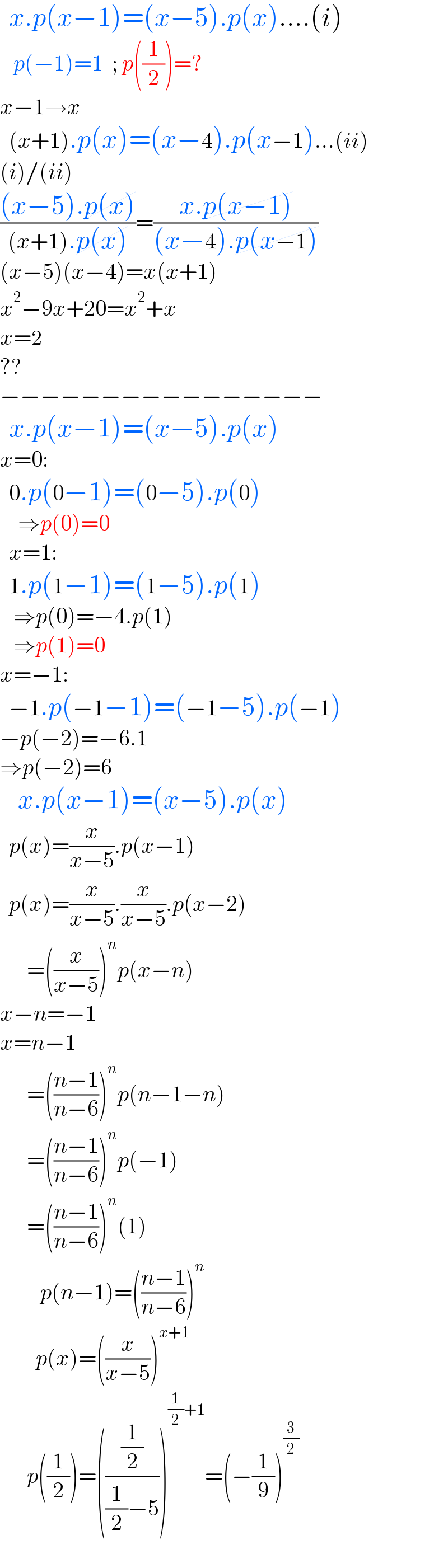
$$\:\:{x}.{p}\left({x}−\mathrm{1}\right)=\left({x}−\mathrm{5}\right).{p}\left({x}\right)....\left({i}\right) \\ $$$$\:\:\:{p}\left(−\mathrm{1}\right)=\mathrm{1}\:\:;\:{p}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=? \\ $$$${x}−\mathrm{1}\rightarrow{x} \\ $$$$\:\:\left({x}+\mathrm{1}\right).{p}\left({x}\right)=\left({x}−\mathrm{4}\right).{p}\left({x}−\mathrm{1}\right)...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right) \\ $$$$\frac{\left({x}−\mathrm{5}\right).\cancel{{p}\left({x}\right)}}{\left({x}+\mathrm{1}\right).\cancel{{p}\left({x}\right)}}=\frac{{x}.\cancel{{p}\left({x}−\mathrm{1}\right)}}{\left({x}−\mathrm{4}\right).\cancel{{p}\left({x}−\mathrm{1}\right)}} \\ $$$$\left({x}−\mathrm{5}\right)\left({x}−\mathrm{4}\right)={x}\left({x}+\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{20}={x}^{\mathrm{2}} +{x} \\ $$$${x}=\mathrm{2} \\ $$$$?? \\ $$$$−−−−−−−−−−−−−−−− \\ $$$$\:\:{x}.{p}\left({x}−\mathrm{1}\right)=\left({x}−\mathrm{5}\right).{p}\left({x}\right) \\ $$$${x}=\mathrm{0}: \\ $$$$\:\:\mathrm{0}.{p}\left(\mathrm{0}−\mathrm{1}\right)=\left(\mathrm{0}−\mathrm{5}\right).{p}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\Rightarrow{p}\left(\mathrm{0}\right)=\mathrm{0}\:\:\:\: \\ $$$$\:\:{x}=\mathrm{1}: \\ $$$$\:\:\mathrm{1}.{p}\left(\mathrm{1}−\mathrm{1}\right)=\left(\mathrm{1}−\mathrm{5}\right).{p}\left(\mathrm{1}\right) \\ $$$$\:\:\:\Rightarrow{p}\left(\mathrm{0}\right)=−\mathrm{4}.{p}\left(\mathrm{1}\right) \\ $$$$\:\:\:\Rightarrow{p}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1}: \\ $$$$\:\:−\mathrm{1}.{p}\left(−\mathrm{1}−\mathrm{1}\right)=\left(−\mathrm{1}−\mathrm{5}\right).{p}\left(−\mathrm{1}\right) \\ $$$$−{p}\left(−\mathrm{2}\right)=−\mathrm{6}.\mathrm{1} \\ $$$$\Rightarrow{p}\left(−\mathrm{2}\right)=\mathrm{6} \\ $$$$\:\:\:\:{x}.{p}\left({x}−\mathrm{1}\right)=\left({x}−\mathrm{5}\right).{p}\left({x}\right) \\ $$$$\:\:{p}\left({x}\right)=\frac{{x}}{{x}−\mathrm{5}}.{p}\left({x}−\mathrm{1}\right) \\ $$$$\:\:{p}\left({x}\right)=\frac{{x}}{{x}−\mathrm{5}}.\frac{{x}}{{x}−\mathrm{5}}.{p}\left({x}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:=\left(\frac{{x}}{{x}−\mathrm{5}}\right)^{{n}} {p}\left({x}−{n}\right) \\ $$$${x}−{n}=−\mathrm{1} \\ $$$${x}={n}−\mathrm{1} \\ $$$$\:\:\:\:\:\:=\left(\frac{{n}−\mathrm{1}}{{n}−\mathrm{6}}\right)^{{n}} {p}\left({n}−\mathrm{1}−{n}\right) \\ $$$$\:\:\:\:\:\:=\left(\frac{{n}−\mathrm{1}}{{n}−\mathrm{6}}\right)^{{n}} {p}\left(−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:=\left(\frac{{n}−\mathrm{1}}{{n}−\mathrm{6}}\right)^{{n}} \left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{p}\left({n}−\mathrm{1}\right)=\left(\frac{{n}−\mathrm{1}}{{n}−\mathrm{6}}\right)^{{n}} \\ $$$$\:\:\:\:\:\:\:\:{p}\left({x}\right)=\left(\frac{{x}}{{x}−\mathrm{5}}\right)^{{x}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:{p}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{5}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}} =\left(−\frac{\mathrm{1}}{\mathrm{9}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$ \\ $$
Commented by mr W last updated on 02/Jan/22
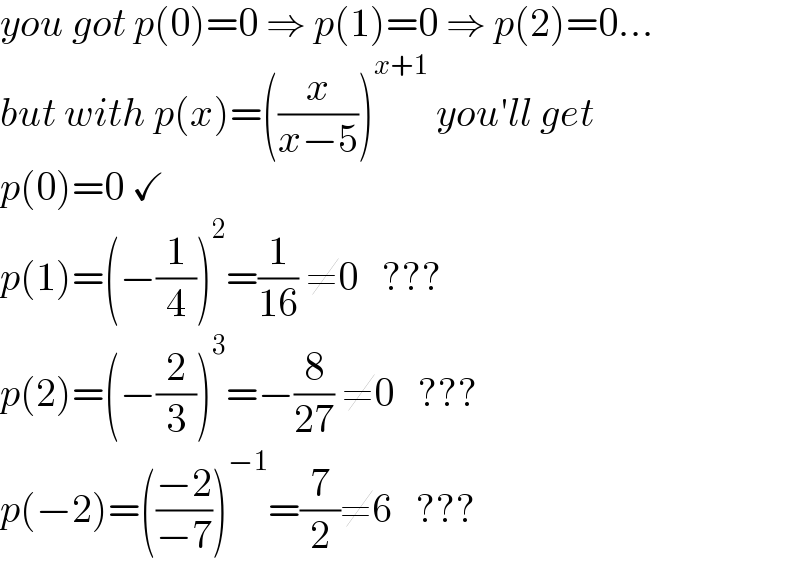
$${you}\:{got}\:{p}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:{p}\left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\:{p}\left(\mathrm{2}\right)=\mathrm{0}... \\ $$$${but}\:{with}\:{p}\left({x}\right)=\left(\frac{{x}}{{x}−\mathrm{5}}\right)^{{x}+\mathrm{1}} \:{you}'{ll}\:{get} \\ $$$${p}\left(\mathrm{0}\right)=\mathrm{0}\:\checkmark \\ $$$${p}\left(\mathrm{1}\right)=\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{16}}\:\neq\mathrm{0}\:\:\:??? \\ $$$${p}\left(\mathrm{2}\right)=\left(−\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} =−\frac{\mathrm{8}}{\mathrm{27}}\:\neq\mathrm{0}\:\:\:??? \\ $$$${p}\left(−\mathrm{2}\right)=\left(\frac{−\mathrm{2}}{−\mathrm{7}}\right)^{−\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{2}}\neq\mathrm{6}\:\:\:??? \\ $$
Commented by Rasheed.Sindhi last updated on 02/Jan/22

$$\mathcal{S}{ir},{I}\:{think}\:{there}'{s}\:{a}\:{serious}\:{error} \\ $$$${either}\:{in}\:{my}\:{answer}\:{or}\:{in}\:{the}\:{question}. \\ $$$${Actually}\:{I}'{ve}\:{no}\:{foundation}\:{regarding} \\ $$$${these}\:{kind}\:{of}\:{questions}.{So}\:{I}'{m}\:{not} \\ $$$${much}\:{confident}.\:\left({I}\:{encountered}\right. \\ $$$$\left.\:{them}\:{only}\:{in}\:{this}\:{forum}\:{only}\right). \\ $$$${Special}\:\mathcal{THANKS}\:{to}\:{you}\:{to}\:{see}\:{my} \\ $$$$\:{answer}/{comments}\:{in}\:{this}\:{critic} \\ $$$$\:{way}\:{by}\:{which}\:{I}\:{could}\:\boldsymbol{{learn}}.{I}\:{have} \\ $$$${feelings}\:{of}\:{your}\:{busyness}\:{in}\:{more} \\ $$$${important}\:{questions}/{work}! \\ $$
Commented by Rasheed.Sindhi last updated on 02/Jan/22
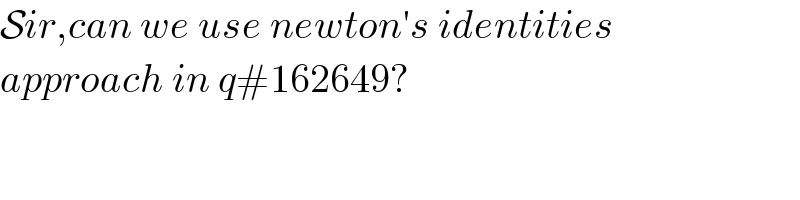
$$\mathcal{S}{ir},{can}\:{we}\:{use}\:{newton}'{s}\:{identities} \\ $$$${approach}\:{in}\:{q}#\mathrm{162649}? \\ $$
Commented by mr W last updated on 02/Jan/22
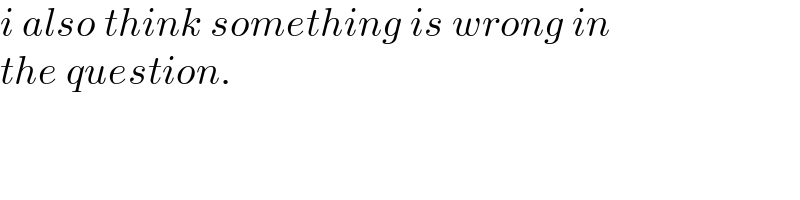
$${i}\:{also}\:{think}\:{something}\:{is}\:{wrong}\:{in} \\ $$$${the}\:{question}. \\ $$
Commented by mr W last updated on 02/Jan/22
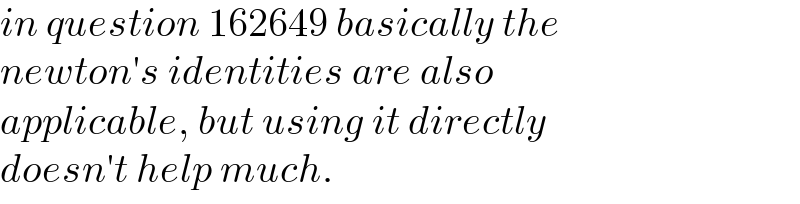
$${in}\:{question}\:\mathrm{162649}\:{basically}\:{the} \\ $$$${newton}'{s}\:{identities}\:{are}\:{also}\: \\ $$$${applicable},\:{but}\:{using}\:{it}\:{directly} \\ $$$${doesn}'{t}\:{help}\:{much}. \\ $$
Commented by Rasheed.Sindhi last updated on 02/Jan/22

$$\mathbb{THANKS}\:\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}\:\mathcal{SIR}! \\ $$
Commented by mr W last updated on 02/Jan/22
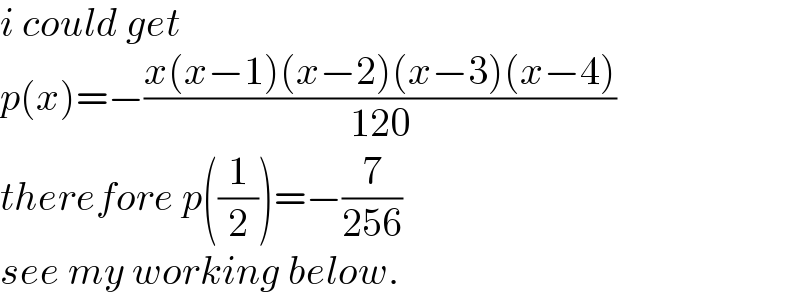
$${i}\:{could}\:{get} \\ $$$${p}\left({x}\right)=−\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}{\mathrm{120}} \\ $$$${therefore}\:{p}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\mathrm{7}}{\mathrm{256}} \\ $$$${see}\:{my}\:{working}\:{below}. \\ $$
