Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 122821 by bemath last updated on 19/Nov/20

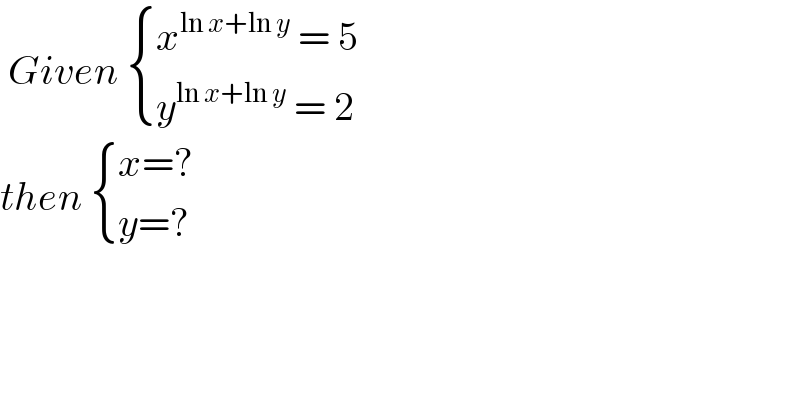
Given { ((x^(ln x+ln y) = 5)),((y^(ln x+ln y) = 2)) :} then { ((x=?)),((y=?)) :}

$$\:{Given}\:\begin{cases}{{x}^{\mathrm{ln}\:{x}+\mathrm{ln}\:{y}} \:=\:\mathrm{5}}\\{{y}^{\mathrm{ln}\:{x}+\mathrm{ln}\:{y}} \:=\:\mathrm{2}}\end{cases} \\ $$$${then}\:\begin{cases}{{x}=?}\\{{y}=?}\end{cases} \\ $$

Answered by liberty last updated on 20/Nov/20

{ ((ln (xy).ln (x) = ln (5) )),((ln (xy).ln (y) = ln (2))) :} → ((ln (5))/(ln (x))) = ((ln (2))/(ln (y))) ⇒ ln (y)=((ln (2))/(ln (5))).ln (x) ⇒ { ln (x)+((ln (2))/(ln (5))).ln (x)}.{((ln (2))/(ln (5))).ln (x)}=ln (2) ln^2 (x) [ 1+((ln (2))/(ln (5))) ].((ln (2))/(ln (5))) = ln (2) ln^2 (x) [ ((ln (10).ln (2))/(ln^2 (5))) ]= ln (2) ln^2 (x) = ((ln^2 (5))/(ln (10))) ⇒ln (x) = ± ((ln (5))/( (√(ln (10))))) ⇒x = e^(± (((ln (5))/( (√(ln (10))))))) .

$$\:\begin{cases}{\mathrm{ln}\:\left({xy}\right).\mathrm{ln}\:\left({x}\right)\:=\:\mathrm{ln}\:\left(\mathrm{5}\right)\:}\\{\mathrm{ln}\:\left({xy}\right).\mathrm{ln}\:\left({y}\right)\:=\:\mathrm{ln}\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\rightarrow\:\frac{\mathrm{ln}\:\left(\mathrm{5}\right)}{\mathrm{ln}\:\left({x}\right)}\:=\:\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left({y}\right)}\:\Rightarrow\:\mathrm{ln}\:\left({y}\right)=\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left(\mathrm{5}\right)}.\mathrm{ln}\:\left({x}\right) \\ $$$$\Rightarrow\:\left\{\:\mathrm{ln}\:\left({x}\right)+\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left(\mathrm{5}\right)}.\mathrm{ln}\:\left({x}\right)\right\}.\left\{\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left(\mathrm{5}\right)}.\mathrm{ln}\:\left({x}\right)\right\}=\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)\:\left[\:\mathrm{1}+\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left(\mathrm{5}\right)}\:\right].\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:\left(\mathrm{5}\right)}\:=\:\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)\:\left[\:\frac{\mathrm{ln}\:\left(\mathrm{10}\right).\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{ln}\:^{\mathrm{2}} \left(\mathrm{5}\right)}\:\right]=\:\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{ln}\:^{\mathrm{2}} \left(\mathrm{5}\right)}{\mathrm{ln}\:\left(\mathrm{10}\right)}\:\Rightarrow\mathrm{ln}\:\left({x}\right)\:=\:\pm\:\frac{\mathrm{ln}\:\left(\mathrm{5}\right)}{\:\sqrt{\mathrm{ln}\:\left(\mathrm{10}\right)}} \\ $$$$\Rightarrow{x}\:=\:{e}^{\pm\:\left(\frac{\mathrm{ln}\:\left(\mathrm{5}\right)}{\:\sqrt{\mathrm{ln}\:\left(\mathrm{10}\right)}}\right)} . \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com