
Question Number 167181 by mathocean1 last updated on 08/Mar/22
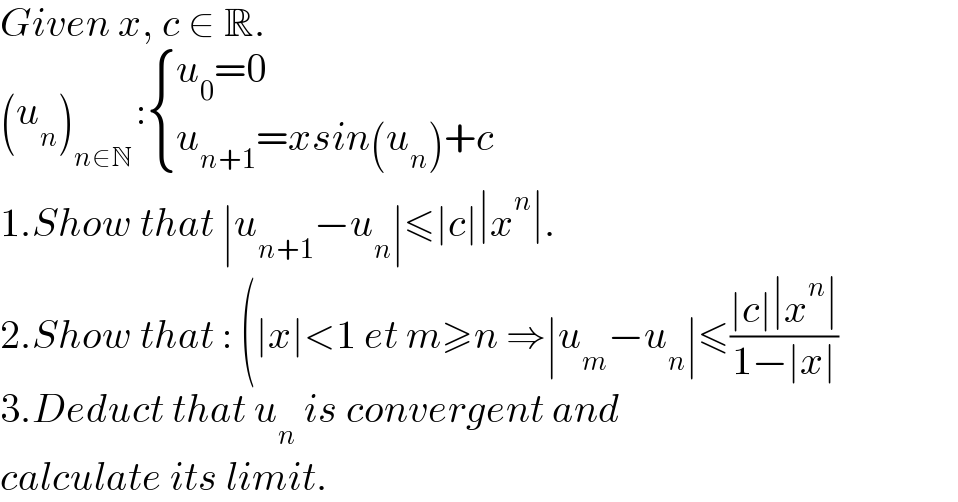
$${Given}\:{x},\:{c}\:\in\:\mathbb{R}. \\ $$$$\left({u}_{{n}} \right)_{{n}\in\mathbb{N}\:} :\begin{cases}{{u}_{\mathrm{0}} =\mathrm{0}}\\{{u}_{{n}+\mathrm{1}} ={xsin}\left({u}_{{n}} \right)+{c}}\end{cases} \\ $$$$\mathrm{1}.{Show}\:{that}\:\mid{u}_{{n}+\mathrm{1}} −{u}_{{n}} \mid\leqslant\mid{c}\mid\mid{x}^{{n}} \mid. \\ $$$$\mathrm{2}.{Show}\:{that}\::\:\left(\mid{x}\mid<\mathrm{1}\:{et}\:{m}\geqslant{n}\:\Rightarrow\mid{u}_{{m}} −{u}_{{n}} \mid\leqslant\frac{\mid{c}\mid\mid{x}^{{n}} \mid}{\mathrm{1}−\mid{x}\mid}\right. \\ $$$$\mathrm{3}.{Deduct}\:{that}\:{u}_{{n}} \:{is}\:{convergent}\:{and} \\ $$$${calculate}\:{its}\:{limit}. \\ $$
Answered by mindispower last updated on 09/Mar/22

$${n}=\mathrm{0} \\ $$$$\mid{U}_{\mathrm{1}} −{U}_{\mathrm{0}} \mid=\mid{c}\mid\:{True} \\ $$$${suppose}\:\forall{n}\:\mid{U}_{{n}+\mathrm{1}} −{U}_{{n}} \mid<\mid{c}\mid\mid{x}^{{n}} \mid \\ $$$${we}\:{show}\:{That}\:\mid{u}_{{n}+\mathrm{2}} −{u}_{{n}+\mathrm{1}} \mid<\mid{c}\mid\mid{x}\mid^{{n}+\mathrm{1}} \\ $$$$\forall{n}\in\mathbb{N}^{\ast} \:\:\mid{U}_{{n}+\mathrm{2}} −{U}_{{n}+\mathrm{1}} \mid=\mid{xsin}\left({u}_{{n}+\mathrm{1}} \right)−{xsin}\left({u}_{{n}} \right)\mid \\ $$$$=\mid{x}\mid.\mid{sin}\left({U}_{{n}+\mathrm{1}} \right)−{sin}\left({U}_{{n}} \right)\mid....\left({E}\right) \\ $$$$\forall\left({a},{b}\right)\in\mathbb{R}^{\mathrm{2}} \:{We}\:{have} \\ $$$$\mid{sin}\left({a}\right)−{sin}\left({b}\right)\mid<\mid{a}−{b}\mid \\ $$$$\left({E}\right)\leqslant\mid{x}\mid.\mid{U}_{{n}+\mathrm{1}} −{U}_{{n}} \mid\leqslant\mid{x}\mid.\mid{c}\mid.\mid{x}\mid^{{n}} =\mid{c}\mid\mid{x}^{{n}+\mathrm{1}} \:{true} \\ $$$$\left(\mathrm{2}\right)\:{use}\:{m}={n}+{k} \\ $$$${and}\:\mid{U}_{{m}} −{U}_{{n}} \mid=\mid\underset{{k}={n}} {\overset{{m}−\mathrm{1}} {\sum}}{U}_{{k}+\mathrm{1}} −{U}_{{k}} \mid<\Sigma\mid{U}_{{k}+\mathrm{1}} −{U}_{{k}} \mid\:{and}\:{Quatiom}\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
