
Question Number 104727 by bemath last updated on 23/Jul/20
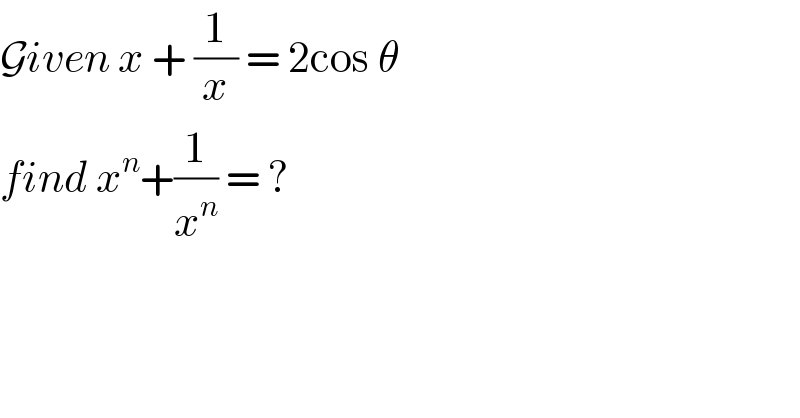
$$\mathcal{G}{iven}\:{x}\:+\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{2cos}\:\theta \\ $$$${find}\:{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\:=\:? \\ $$
Commented by bemath last updated on 23/Jul/20

$${thank}\:{you}\:{all} \\ $$
Answered by mr W last updated on 23/Jul/20
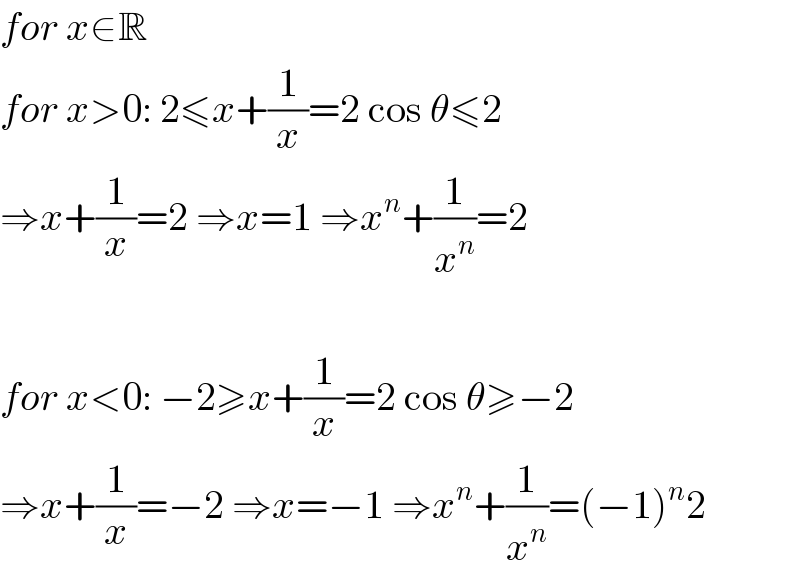
$${for}\:{x}\in\mathbb{R} \\ $$$${for}\:{x}>\mathrm{0}:\:\mathrm{2}\leqslant{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}\:\mathrm{cos}\:\theta\leqslant\mathrm{2} \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}\:\Rightarrow{x}=\mathrm{1}\:\Rightarrow{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\mathrm{2} \\ $$$$ \\ $$$${for}\:{x}<\mathrm{0}:\:−\mathrm{2}\geqslant{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}\:\mathrm{cos}\:\theta\geqslant−\mathrm{2} \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=−\mathrm{2}\:\Rightarrow{x}=−\mathrm{1}\:\Rightarrow{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\left(−\mathrm{1}\right)^{{n}} \mathrm{2} \\ $$
Commented by 1549442205PVT last updated on 23/Jul/20

$$\mathrm{Great}\:\mathrm{Sir}! \\ $$
Answered by john santu last updated on 23/Jul/20

$${we}\:{solve}\:{the}\:{given}\:{equation}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{cos}\:\theta\:+\mathrm{1}\:=\:\mathrm{0}\:{for}\:{x}\:.\:{Discriminat}\: \\ $$$$\Delta=\:\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{4}\:=\:−\mathrm{4sin}\:^{\mathrm{2}} \theta \\ $$$${so}\:{the}\:{roots}\:{are}\:\mathrm{cos}\:\theta\:\pm\:{i}\:\mathrm{sin}\:\theta \\ $$$${By}\:{De}\:{Moivre}'{s}\:{formula} \\ $$$${x}^{{n}} \:=\:\mathrm{cos}\:\left({n}\theta\right)\:+{i}\:\mathrm{sin}\:\left({n}\theta\right) \\ $$$${x}^{−{n}} \:=\:\mathrm{cos}\:\left(−{n}\theta\right)+{i}\:\mathrm{sin}\:\left(−{n}\theta\right) \\ $$$${and}\:{therefore}\: \\ $$$${x}^{{n}} \:+{x}^{−{n}} \:=\:\left\{\mathrm{cos}\:\left({n}\theta\right)+{i}\:\mathrm{sin}\:\left({n}\theta\right)\right\}\:+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\:\mathrm{cos}\:\left(−{n}\theta\right)+{i}\:\mathrm{sin}\:\left(−{n}\theta\right)\right\} \\ $$$${x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\:=\:\mathrm{2cos}\:\left({n}\theta\right)\: \\ $$$$\left({JS}\:\circledast\:\right)\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jul/20
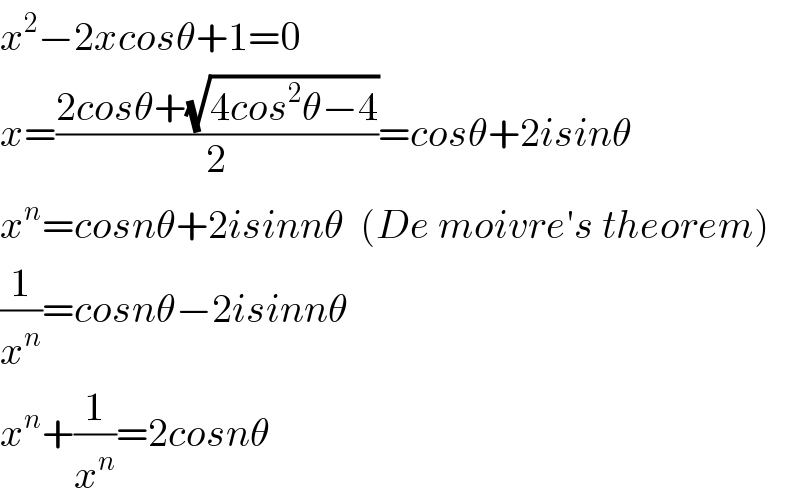
$${x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}{cos}\theta+\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \theta−\mathrm{4}}}{\mathrm{2}}={cos}\theta+\mathrm{2}{isin}\theta \\ $$$${x}^{{n}} ={cosn}\theta+\mathrm{2}{isinn}\theta\:\:\left({De}\:{moivre}'{s}\:{theorem}\right) \\ $$$$\frac{\mathrm{1}}{{x}^{{n}} }={cosn}\theta−\mathrm{2}{isinn}\theta \\ $$$${x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\mathrm{2}{cosn}\theta \\ $$
Answered by mathmax by abdo last updated on 24/Jul/20
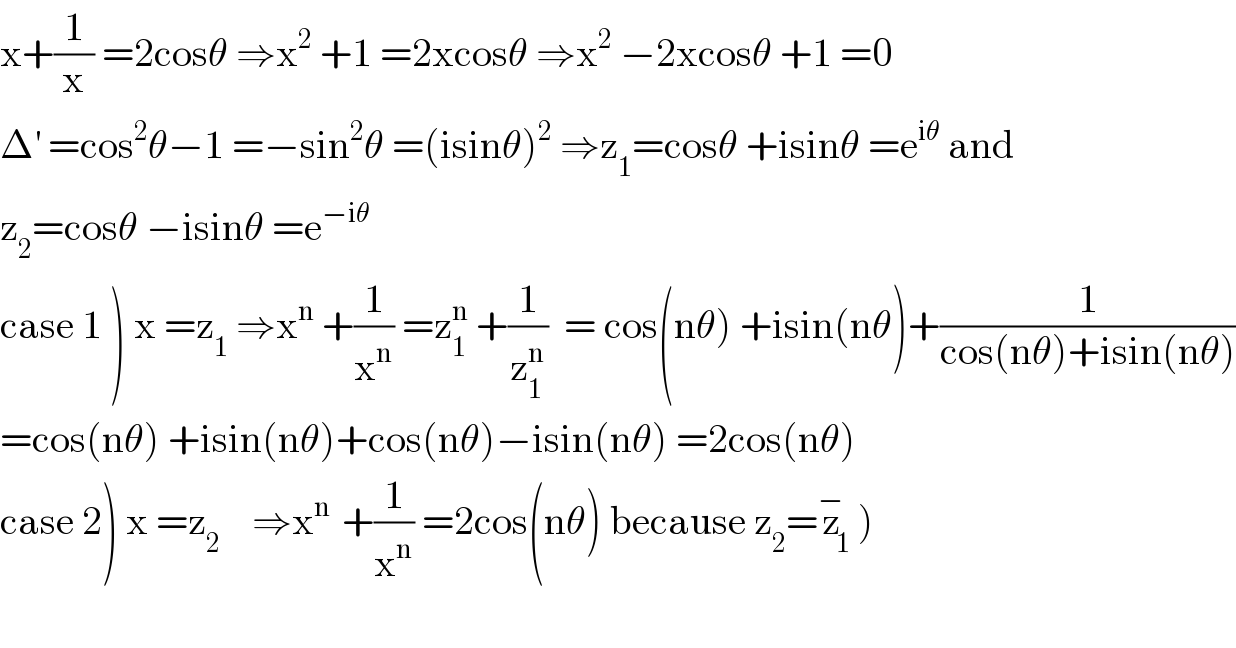
$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{2cos}\theta\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{2xcos}\theta\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:−\mathrm{2xcos}\theta\:+\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{1}\:=−\mathrm{sin}^{\mathrm{2}} \theta\:=\left(\mathrm{isin}\theta\right)^{\mathrm{2}} \:\Rightarrow\mathrm{z}_{\mathrm{1}} =\mathrm{cos}\theta\:+\mathrm{isin}\theta\:=\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{and} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{cos}\theta\:−\mathrm{isin}\theta\:=\mathrm{e}^{−\mathrm{i}\theta} \\ $$$$\left.\mathrm{case}\:\mathrm{1}\:\right)\:\mathrm{x}\:=\mathrm{z}_{\mathrm{1}} \:\Rightarrow\mathrm{x}^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:=\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} }\:\:=\:\mathrm{cos}\left(\mathrm{n}\theta\right)\:+\mathrm{isin}\left(\mathrm{n}\theta\right)+\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{n}\theta\right)+\mathrm{isin}\left(\mathrm{n}\theta\right)} \\ $$$$=\mathrm{cos}\left(\mathrm{n}\theta\right)\:+\mathrm{isin}\left(\mathrm{n}\theta\right)+\mathrm{cos}\left(\mathrm{n}\theta\right)−\mathrm{isin}\left(\mathrm{n}\theta\right)\:=\mathrm{2cos}\left(\mathrm{n}\theta\right) \\ $$$$\left.\mathrm{c}\left.\mathrm{ase}\:\mathrm{2}\right)\:\mathrm{x}\:=\mathrm{z}_{\mathrm{2}} \:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{n}\:} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:=\mathrm{2cos}\left(\mathrm{n}\theta\right)\:\mathrm{because}\:\mathrm{z}_{\mathrm{2}} =\overset{−} {\mathrm{z}}_{\mathrm{1}} \right) \\ $$$$ \\ $$
