
Question Number 164478 by mathocean1 last updated on 17/Jan/22
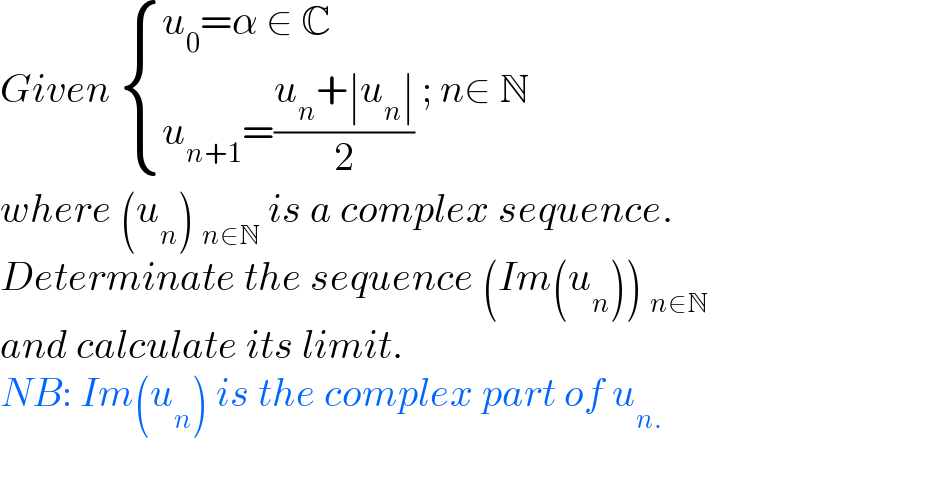
$${Given}\:\begin{cases}{{u}_{\mathrm{0}} =\alpha\:\in\:\mathbb{C}}\\{{u}_{{n}+\mathrm{1}} =\frac{{u}_{{n}} +\mid{u}_{{n}} \mid}{\mathrm{2}}}\end{cases}\:;\:{n}\in\:\mathbb{N} \\ $$$${where}\:\left({u}_{{n}} \right)\:_{{n}\in\mathbb{N}} \:{is}\:{a}\:{complex}\:{sequence}. \\ $$$${Determinate}\:{the}\:{sequence}\:\left({Im}\left({u}_{{n}} \right)\right)\:_{{n}\in\mathbb{N}} \\ $$$${and}\:{calculate}\:{its}\:{limit}. \\ $$$${NB}:\:{Im}\left({u}_{{n}} \right)\:{is}\:{the}\:{complex}\:{part}\:{of}\:{u}_{{n}.} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jan/22
![u_n =a_n +ib_n u_0 =α=a_0 +ib_0 a_(n+1) +ib_(n+1) =((a_n +ib_n +∣a_n +ib_n ∣)/2) a_(n+1) +ib_(n+1) =((a_n +(√(a_n ^2 +b_n ^2 )))/2)+((ib_n )/2) im(u_(n+1) ): b_(n+1) =(b_n /2) ⇒^(n→n−1) b_n =(b_(n−1) /2) b_1 =(b_0 /2) b_2 =(b_1 /2)=((b_0 /2)/2)=(b_0 /2^2 ) b_3 =(b_2 /2)=(b_0 /2^3 ) ... b_n =(b_0 /2^n )=((im(α))/2^n ) lim_(n→∞) b_n = lim_(n→∞) ((im(α))/2^n )=0 [∵ im(α) is constant]](Q164491.png)
$${u}_{{n}} ={a}_{{n}} +{ib}_{{n}} \\ $$$${u}_{\mathrm{0}} =\alpha={a}_{\mathrm{0}} +{ib}_{\mathrm{0}} \\ $$$${a}_{{n}+\mathrm{1}} +{ib}_{{n}+\mathrm{1}} =\frac{{a}_{{n}} +{ib}_{{n}} +\mid{a}_{{n}} +{ib}_{{n}} \mid}{\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} +{ib}_{{n}+\mathrm{1}} =\frac{{a}_{{n}} +\sqrt{{a}_{{n}} ^{\mathrm{2}} +{b}_{{n}} ^{\mathrm{2}} }}{\mathrm{2}}+\frac{{ib}_{{n}} }{\mathrm{2}} \\ $$$${im}\left({u}_{{n}+\mathrm{1}} \right):\:\:\:{b}_{{n}+\mathrm{1}} =\frac{{b}_{{n}} }{\mathrm{2}}\:\:\overset{{n}\rightarrow{n}−\mathrm{1}} {\Rightarrow}\:\:\:\:{b}_{{n}} =\frac{{b}_{{n}−\mathrm{1}} }{\mathrm{2}} \\ $$$${b}_{\mathrm{1}} =\frac{{b}_{\mathrm{0}} }{\mathrm{2}} \\ $$$${b}_{\mathrm{2}} =\frac{{b}_{\mathrm{1}} }{\mathrm{2}}=\frac{\frac{{b}_{\mathrm{0}} }{\mathrm{2}}}{\mathrm{2}}=\frac{{b}_{\mathrm{0}} }{\mathrm{2}^{\mathrm{2}} } \\ $$$${b}_{\mathrm{3}} =\frac{{b}_{\mathrm{2}} }{\mathrm{2}}=\frac{{b}_{\mathrm{0}} }{\mathrm{2}^{\mathrm{3}} } \\ $$$$... \\ $$$${b}_{{n}} =\frac{{b}_{\mathrm{0}} }{\mathrm{2}^{{n}} }=\frac{{im}\left(\alpha\right)}{\mathrm{2}^{{n}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{b}_{{n}} \:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{im}\left(\alpha\right)}{\mathrm{2}^{{n}} }=\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\because\:{im}\left(\alpha\right)\:{is}\:{constant}\right] \\ $$
Commented by mathocean1 last updated on 19/Jan/22

$${thanks} \\ $$
