
Question Number 97781 by Ar Brandon last updated on 09/Jun/20
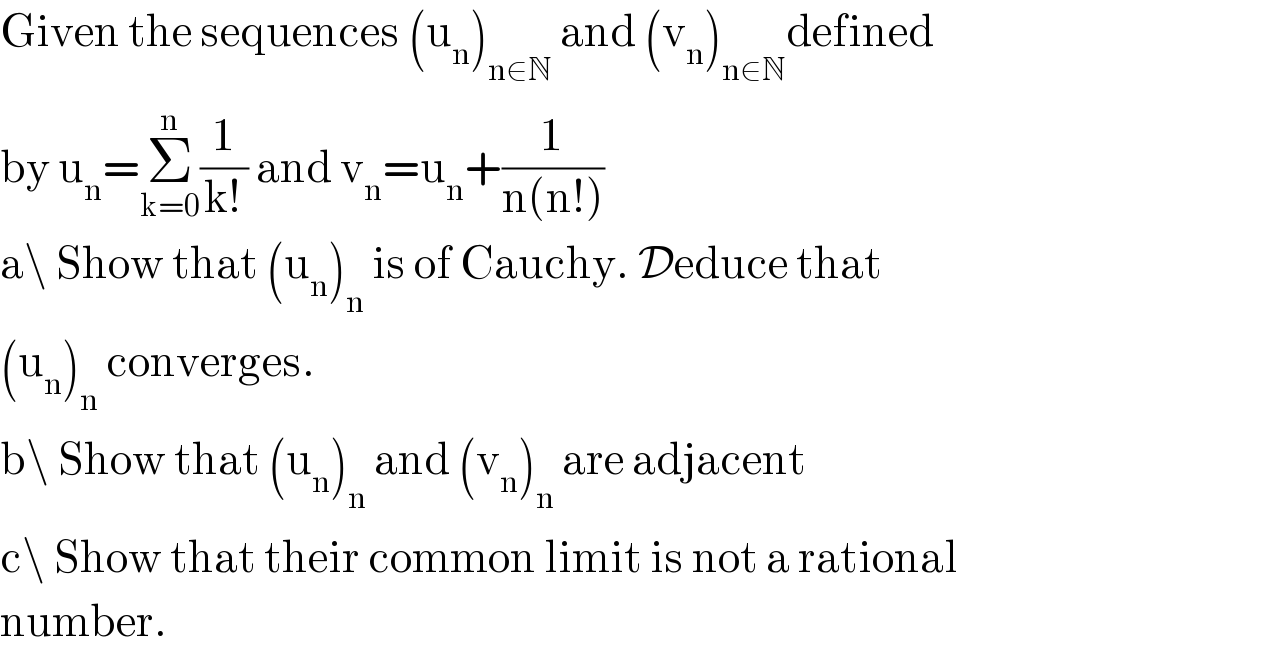
$$\mathrm{Given}\:\mathrm{the}\:\mathrm{sequences}\:\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \:\mathrm{and}\:\left(\mathrm{v}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \mathrm{defined} \\ $$$$\mathrm{by}\:\mathrm{u}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}!}\:\mathrm{and}\:\mathrm{v}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}!\right)} \\ $$$$\mathrm{a}\backslash\:\mathrm{Show}\:\mathrm{that}\:\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}} \:\mathrm{is}\:\mathrm{of}\:\mathrm{Cauchy}.\:\mathcal{D}\mathrm{educe}\:\mathrm{that} \\ $$$$\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}} \:\mathrm{converges}. \\ $$$$\mathrm{b}\backslash\:\mathrm{Show}\:\mathrm{that}\:\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}} \:\mathrm{and}\:\left(\mathrm{v}_{\mathrm{n}} \right)_{\mathrm{n}} \:\mathrm{are}\:\mathrm{adjacent} \\ $$$$\mathrm{c}\backslash\:\mathrm{Show}\:\mathrm{that}\:\mathrm{their}\:\mathrm{common}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{rational} \\ $$$$\mathrm{number}. \\ $$
Answered by maths mind last updated on 10/Jun/20
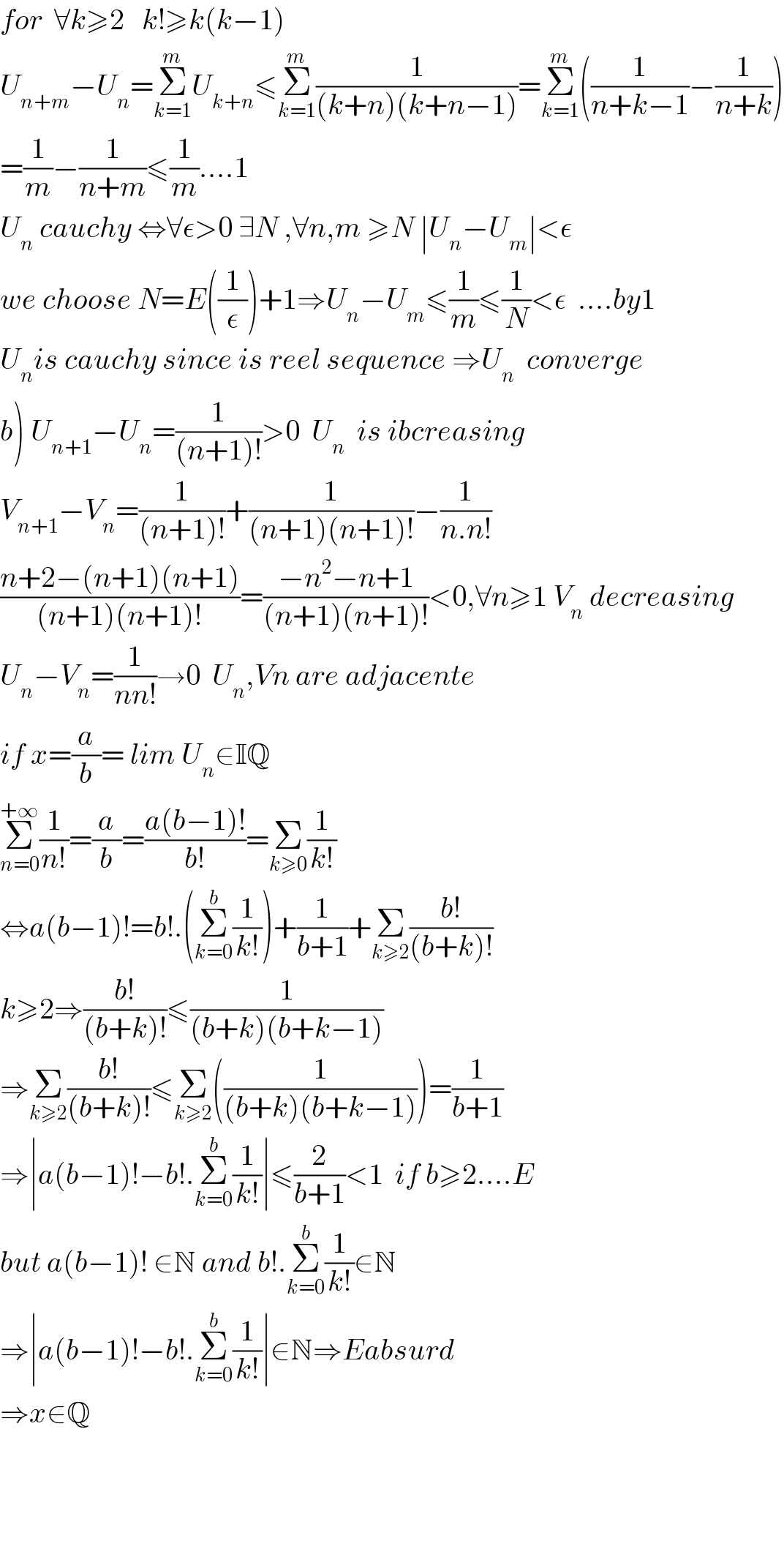
$${for}\:\:\forall{k}\geqslant\mathrm{2}\:\:\:{k}!\geqslant{k}\left({k}−\mathrm{1}\right) \\ $$$${U}_{{n}+{m}} −{U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{U}_{{k}+{n}} \leqslant\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\mathrm{1}}{\left({k}+{n}\right)\left({k}+{n}−\mathrm{1}\right)}=\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\left(\frac{\mathrm{1}}{{n}+{k}−\mathrm{1}}−\frac{\mathrm{1}}{{n}+{k}}\right) \\ $$$$=\frac{\mathrm{1}}{{m}}−\frac{\mathrm{1}}{{n}+{m}}\leqslant\frac{\mathrm{1}}{{m}}....\mathrm{1} \\ $$$${U}_{{n}} \:{cauchy}\:\Leftrightarrow\forall\epsilon>\mathrm{0}\:\exists{N}\:,\forall{n},{m}\:\geqslant{N}\:\mid{U}_{{n}} −{U}_{{m}} \mid<\epsilon \\ $$$${we}\:{choose}\:{N}={E}\left(\frac{\mathrm{1}}{\epsilon}\right)+\mathrm{1}\Rightarrow{U}_{{n}} −{U}_{{m}} \leqslant\frac{\mathrm{1}}{{m}}\leqslant\frac{\mathrm{1}}{{N}}<\epsilon\:\:....{by}\mathrm{1} \\ $$$${U}_{{n}} {is}\:{cauchy}\:{since}\:{is}\:{reel}\:{sequence}\:\Rightarrow{U}_{{n}} \:\:{converge} \\ $$$$\left.{b}\right)\:{U}_{{n}+\mathrm{1}} −{U}_{{n}} =\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}>\mathrm{0}\:\:{U}_{{n}} \:\:{is}\:{ibcreasing} \\ $$$${V}_{{n}+\mathrm{1}} −{V}_{{n}} =\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{{n}.{n}!} \\ $$$$\frac{{n}+\mathrm{2}−\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)!}=\frac{−{n}^{\mathrm{2}} −{n}+\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)!}<\mathrm{0},\forall{n}\geqslant\mathrm{1}\:{V}_{{n}} \:{decreasing} \\ $$$${U}_{{n}} −{V}_{{n}} =\frac{\mathrm{1}}{{nn}!}\rightarrow\mathrm{0}\:\:{U}_{{n}} ,{Vn}\:{are}\:{adjacente} \\ $$$${if}\:{x}=\frac{{a}}{{b}}=\:{lim}\:{U}_{{n}} \in\mathbb{IQ}\:\: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\frac{{a}}{{b}}=\frac{{a}\left({b}−\mathrm{1}\right)!}{{b}!}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{k}!} \\ $$$$\Leftrightarrow{a}\left({b}−\mathrm{1}\right)!={b}!.\left(\underset{{k}=\mathrm{0}} {\overset{{b}} {\sum}}\frac{\mathrm{1}}{{k}!}\right)+\frac{\mathrm{1}}{{b}+\mathrm{1}}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{b}!}{\left({b}+{k}\right)!} \\ $$$${k}\geqslant\mathrm{2}\Rightarrow\frac{{b}!}{\left({b}+{k}\right)!}\leqslant\frac{\mathrm{1}}{\left({b}+{k}\right)\left({b}+{k}−\mathrm{1}\right)} \\ $$$$\Rightarrow\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{b}!}{\left({b}+{k}\right)!}\leqslant\underset{{k}\geqslant\mathrm{2}} {\sum}\left(\frac{\mathrm{1}}{\left({b}+{k}\right)\left({b}+{k}−\mathrm{1}\right)}\right)=\frac{\mathrm{1}}{{b}+\mathrm{1}} \\ $$$$\Rightarrow\mid{a}\left({b}−\mathrm{1}\right)!−{b}!.\underset{{k}=\mathrm{0}} {\overset{{b}} {\sum}}\frac{\mathrm{1}}{{k}!}\mid\leqslant\frac{\mathrm{2}}{{b}+\mathrm{1}}<\mathrm{1}\:\:{if}\:{b}\geqslant\mathrm{2}....{E} \\ $$$${but}\:{a}\left({b}−\mathrm{1}\right)!\:\in\mathbb{N}\:{and}\:{b}!.\underset{{k}=\mathrm{0}} {\overset{{b}} {\sum}}\frac{\mathrm{1}}{{k}!}\in\mathbb{N} \\ $$$$\Rightarrow\mid{a}\left({b}−\mathrm{1}\right)!−{b}!.\underset{{k}=\mathrm{0}} {\overset{{b}} {\sum}}\frac{\mathrm{1}}{{k}!}\mid\in\mathbb{N}\Rightarrow{Eabsurd} \\ $$$$\Rightarrow{x}\notin\mathbb{Q} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 10/Jun/20

$$\mathcal{T}\mathrm{hanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{method}, \\ $$
