Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 163323 by ZiYangLee last updated on 06/Jan/22

Given the roots of the quadratic equation 4x^2 −4x+5=0 are α and β. f(x) is a quadratic function where f(α)=β , f(β)=α and f(0)=6 . Find f(x).

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0}\:\mathrm{are}\:\alpha\:\mathrm{and}\:\beta.\:\: \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{function}\:\mathrm{where}\:{f}\left(\alpha\right)=\beta\:, \\ $$$${f}\left(\beta\right)=\alpha\:\mathrm{and}\:{f}\left(\mathrm{0}\right)=\mathrm{6}\:.\: \\ $$$$\mathrm{Find}\:{f}\left({x}\right). \\ $$

Commented by cortano1 last updated on 06/Jan/22

let f(x)= px^2 +qx+6 ⇒ { ((f(α)=pα^2 +qα+6=β)),((f(β)=pβ^2 +qβ+6=α)) :} (1)+(2)⇒p[(α+β)^2 −2αβ ]+q(α+β)+12=α+β ⇒p[ 1−(5/2) ]+q(1)+12=1 ⇒−(3/2)p+q=−11 ⇒−3p+2q=−22 ⇒q=((3p−22)/2) ∴ f(x)= px^2 +(((3p−22)/2))x+6

$${let}\:{f}\left({x}\right)=\:{px}^{\mathrm{2}} +{qx}+\mathrm{6}\: \\ $$$$\Rightarrow\begin{cases}{{f}\left(\alpha\right)={p}\alpha^{\mathrm{2}} +{q}\alpha+\mathrm{6}=\beta}\\{{f}\left(\beta\right)={p}\beta^{\mathrm{2}} +{q}\beta+\mathrm{6}=\alpha}\end{cases} \\ $$$$\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow{p}\left[\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\:\right]+{q}\left(\alpha+\beta\right)+\mathrm{12}=\alpha+\beta \\ $$$$\Rightarrow{p}\left[\:\mathrm{1}−\frac{\mathrm{5}}{\mathrm{2}}\:\right]+{q}\left(\mathrm{1}\right)+\mathrm{12}=\mathrm{1} \\ $$$$\Rightarrow−\frac{\mathrm{3}}{\mathrm{2}}{p}+{q}=−\mathrm{11} \\ $$$$\Rightarrow−\mathrm{3}{p}+\mathrm{2}{q}=−\mathrm{22} \\ $$$$\Rightarrow{q}=\frac{\mathrm{3}{p}−\mathrm{22}}{\mathrm{2}} \\ $$$$\therefore\:{f}\left({x}\right)=\:{px}^{\mathrm{2}} +\left(\frac{\mathrm{3}{p}−\mathrm{22}}{\mathrm{2}}\right){x}+\mathrm{6}\: \\ $$

Answered by Rasheed.Sindhi last updated on 06/Jan/22

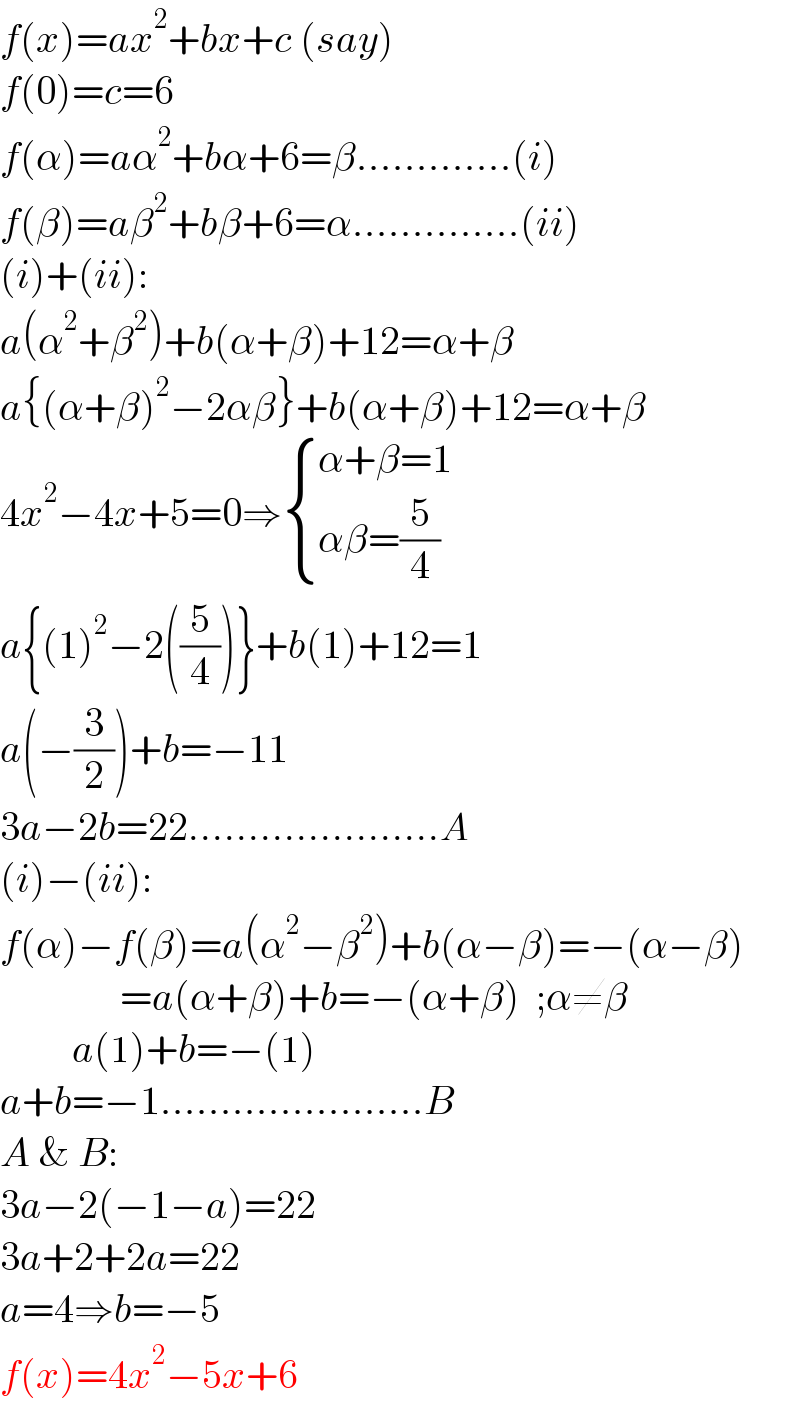
f(x)=ax^2 +bx+c (say) f(0)=c=6 f(α)=aα^2 +bα+6=β.............(i) f(β)=aβ^2 +bβ+6=α..............(ii) (i)+(ii): a(α^2 +β^2 )+b(α+β)+12=α+β a{(α+β)^2 −2αβ}+b(α+β)+12=α+β 4x^2 −4x+5=0⇒ { ((α+β=1)),((αβ=(5/4))) :} a{(1)^2 −2((5/4))}+b(1)+12=1 a(−(3/2))+b=−11 3a−2b=22.....................A (i)−(ii): f(α)−f(β)=a(α^2 −β^2 )+b(α−β)=−(α−β) =a(α+β)+b=−(α+β) ;α≠β a(1)+b=−(1) a+b=−1......................B A & B: 3a−2(−1−a)=22 3a+2+2a=22 a=4⇒b=−5 f(x)=4x^2 −5x+6

$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}\:\left({say}\right) \\ $$$${f}\left(\mathrm{0}\right)={c}=\mathrm{6} \\ $$$${f}\left(\alpha\right)={a}\alpha^{\mathrm{2}} +{b}\alpha+\mathrm{6}=\beta.............\left({i}\right) \\ $$$${f}\left(\beta\right)={a}\beta^{\mathrm{2}} +{b}\beta+\mathrm{6}=\alpha..............\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${a}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)+{b}\left(\alpha+\beta\right)+\mathrm{12}=\alpha+\beta \\ $$$${a}\left\{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\right\}+{b}\left(\alpha+\beta\right)+\mathrm{12}=\alpha+\beta \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0}\Rightarrow\begin{cases}{\alpha+\beta=\mathrm{1}}\\{\alpha\beta=\frac{\mathrm{5}}{\mathrm{4}}}\end{cases} \\ $$$${a}\left\{\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\right\}+{b}\left(\mathrm{1}\right)+\mathrm{12}=\mathrm{1} \\ $$$${a}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)+{b}=−\mathrm{11} \\ $$$$\mathrm{3}{a}−\mathrm{2}{b}=\mathrm{22}.....................{A} \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${f}\left(\alpha\right)−{f}\left(\beta\right)={a}\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)+{b}\left(\alpha−\beta\right)=−\left(\alpha−\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}\left(\alpha+\beta\right)+{b}=−\left(\alpha+\beta\right)\:\:;\alpha\neq\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{a}\left(\mathrm{1}\right)+{b}=−\left(\mathrm{1}\right) \\ $$$${a}+{b}=−\mathrm{1}......................{B} \\ $$$${A}\:\&\:{B}: \\ $$$$\mathrm{3}{a}−\mathrm{2}\left(−\mathrm{1}−{a}\right)=\mathrm{22} \\ $$$$\mathrm{3}{a}+\mathrm{2}+\mathrm{2}{a}=\mathrm{22} \\ $$$${a}=\mathrm{4}\Rightarrow{b}=−\mathrm{5} \\ $$$${f}\left({x}\right)=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6} \\ $$

Commented by peter frank last updated on 06/Jan/22

great

$$\mathrm{great} \\ $$

Commented by Rasheed.Sindhi last updated on 06/Jan/22

Thank you Peter sir!

$$\mathcal{T}{hank}\:{you}\:{Peter}\:{sir}! \\ $$

Commented by Tawa11 last updated on 06/Jan/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com