
Question Number 37661 by Rio Mike last updated on 16/Jun/18
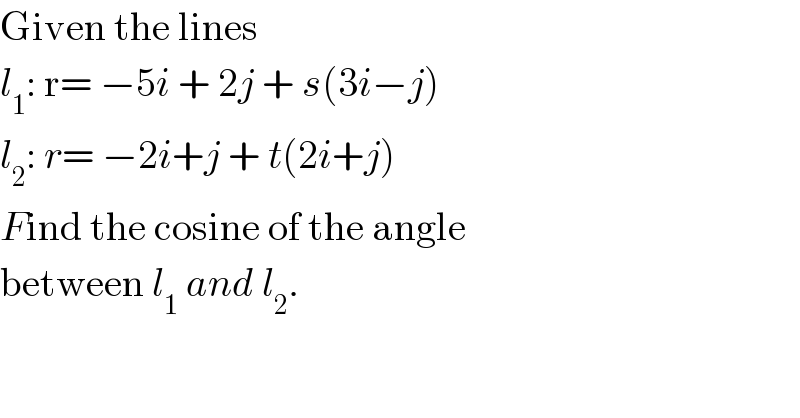
$$\mathrm{Given}\:\mathrm{the}\:\mathrm{lines}\: \\ $$$${l}_{\mathrm{1}} :\:\mathrm{r}=\:−\mathrm{5}{i}\:+\:\mathrm{2}{j}\:+\:{s}\left(\mathrm{3}{i}−{j}\right) \\ $$$${l}_{\mathrm{2}} :\:{r}=\:−\mathrm{2}{i}+{j}\:+\:{t}\left(\mathrm{2}{i}+{j}\right) \\ $$$${F}\mathrm{ind}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{of}\:\mathrm{the}\:\mathrm{angle} \\ $$$$\mathrm{between}\:{l}_{\mathrm{1}} \:{and}\:{l}_{\mathrm{2}} . \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jun/18
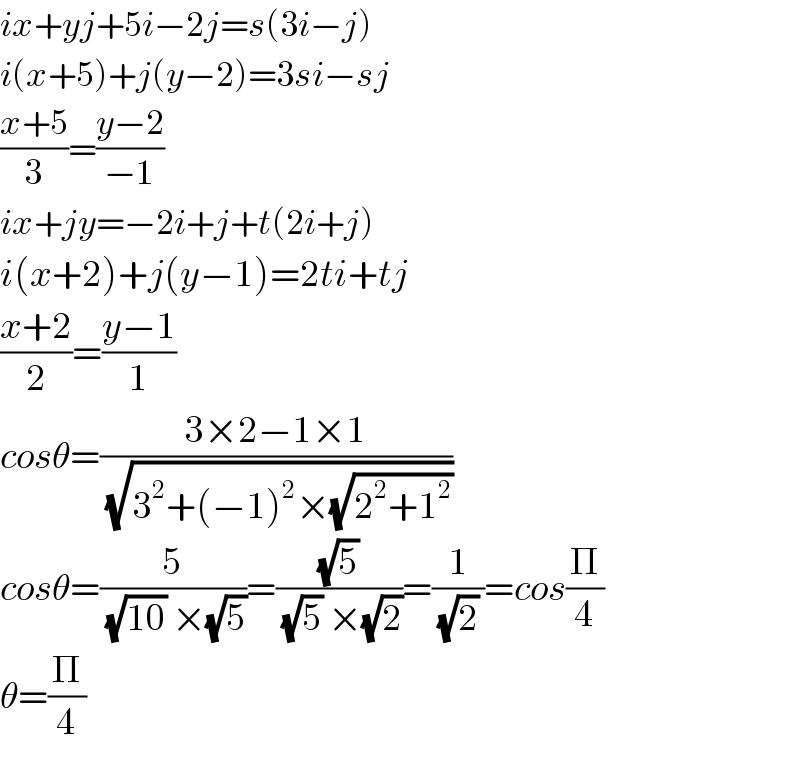
$${ix}+{yj}+\mathrm{5}{i}−\mathrm{2}{j}={s}\left(\mathrm{3}{i}−{j}\right) \\ $$$${i}\left({x}+\mathrm{5}\right)+{j}\left({y}−\mathrm{2}\right)=\mathrm{3}{si}−{sj} \\ $$$$\frac{{x}+\mathrm{5}}{\mathrm{3}}=\frac{{y}−\mathrm{2}}{−\mathrm{1}} \\ $$$${ix}+{jy}=−\mathrm{2}{i}+{j}+{t}\left(\mathrm{2}{i}+{j}\right) \\ $$$${i}\left({x}+\mathrm{2}\right)+{j}\left({y}−\mathrm{1}\right)=\mathrm{2}{ti}+{tj} \\ $$$$\frac{{x}+\mathrm{2}}{\mathrm{2}}=\frac{{y}−\mathrm{1}}{\mathrm{1}} \\ $$$${cos}\theta=\frac{\mathrm{3}×\mathrm{2}−\mathrm{1}×\mathrm{1}}{\sqrt{\mathrm{3}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} ×\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}} \\ $$$${cos}\theta=\frac{\mathrm{5}}{\sqrt{\mathrm{10}}\:×\sqrt{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}\:×\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}={cos}\frac{\Pi}{\mathrm{4}} \\ $$$$\theta=\frac{\Pi}{\mathrm{4}} \\ $$
