Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 43353 by pieroo last updated on 10/Sep/18

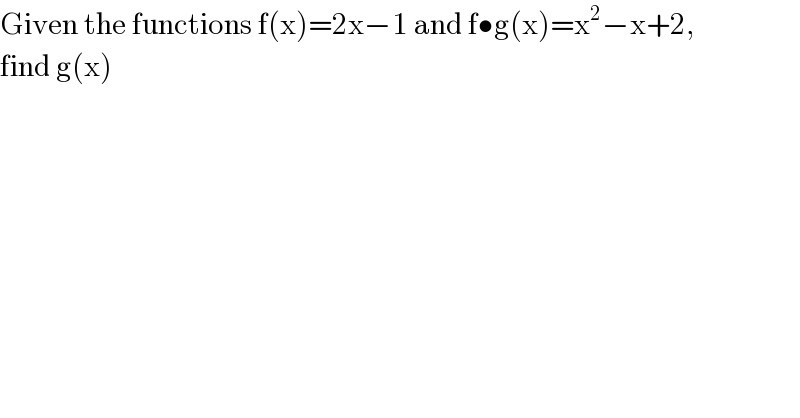
Given the functions f(x)=2x−1 and f•g(x)=x^2 −x+2, find g(x)

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{functions}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{1}\:\mathrm{and}\:\mathrm{f}\bullet\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}, \\ $$$$\mathrm{find}\:\mathrm{g}\left(\mathrm{x}\right) \\ $$

Commented by maxmathsup by imad last updated on 10/Sep/18

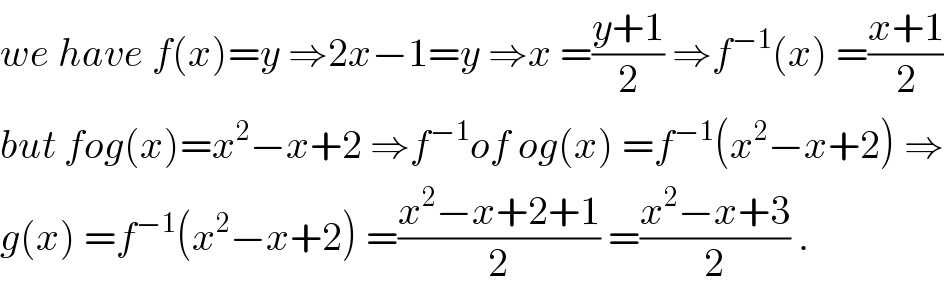
we have f(x)=y ⇒2x−1=y ⇒x =((y+1)/2) ⇒f^(−1) (x) =((x+1)/2) but fog(x)=x^2 −x+2 ⇒f^(−1) of og(x) =f^(−1) (x^2 −x+2) ⇒ g(x) =f^(−1) (x^2 −x+2) =((x^2 −x+2+1)/2) =((x^2 −x+3)/2) .

$${we}\:{have}\:{f}\left({x}\right)={y}\:\Rightarrow\mathrm{2}{x}−\mathrm{1}={y}\:\Rightarrow{x}\:=\frac{{y}+\mathrm{1}}{\mathrm{2}}\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)\:=\frac{{x}+\mathrm{1}}{\mathrm{2}} \\ $$$${but}\:{fog}\left({x}\right)={x}^{\mathrm{2}} −{x}+\mathrm{2}\:\Rightarrow{f}^{−\mathrm{1}} {of}\:{og}\left({x}\right)\:={f}^{−\mathrm{1}} \left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\:\Rightarrow \\ $$$${g}\left({x}\right)\:={f}^{−\mathrm{1}} \left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\:=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{2}+\mathrm{1}}{\mathrm{2}}\:=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{\mathrm{2}}\:. \\ $$

Answered by Joel578 last updated on 10/Sep/18

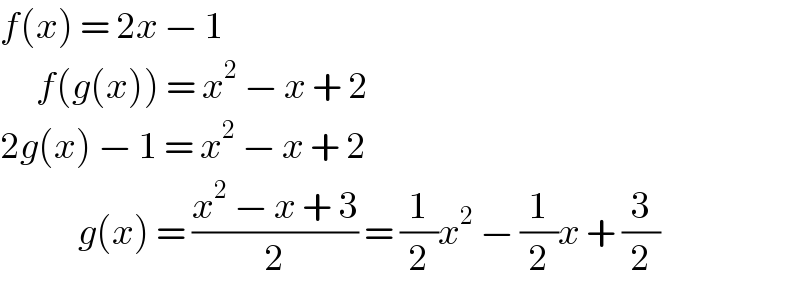
f(x) = 2x − 1 f(g(x)) = x^2 − x + 2 2g(x) − 1 = x^2 − x + 2 g(x) = ((x^2 − x + 3)/2) = (1/2)x^2 − (1/2)x + (3/2)

$${f}\left({x}\right)\:=\:\mathrm{2}{x}\:−\:\mathrm{1} \\ $$$$\:\:\:\:\:\:{f}\left({g}\left({x}\right)\right)\:=\:{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{2} \\ $$$$\mathrm{2}{g}\left({x}\right)\:−\:\mathrm{1}\:=\:{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{g}\left({x}\right)\:=\:\frac{{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:−\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

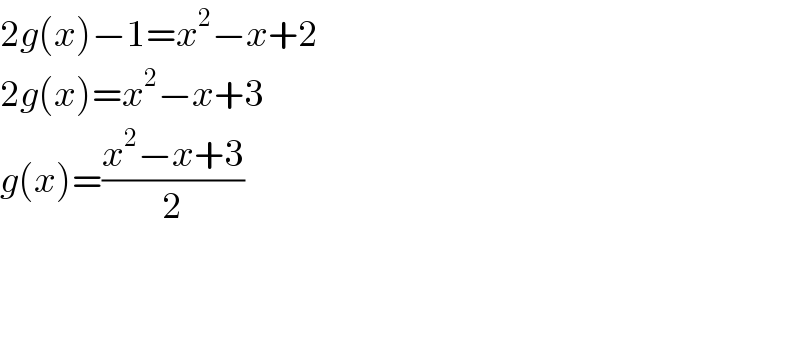
2g(x)−1=x^2 −x+2 2g(x)=x^2 −x+3 g(x)=((x^2 −x+3)/2)

$$\mathrm{2}{g}\left({x}\right)−\mathrm{1}={x}^{\mathrm{2}} −{x}+\mathrm{2} \\ $$$$\mathrm{2}{g}\left({x}\right)={x}^{\mathrm{2}} −{x}+\mathrm{3} \\ $$$${g}\left({x}\right)=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com