Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 107454 by Rio Michael last updated on 10/Aug/20

Given the function f(x) = ((x + 3)/(x−2)) and g(x) = (1/2)xe^x (1) Find the centre of symmetry of f. (2) Define the monotony of g and if possible draw a variation table for g(x). (3) Sketch the function g(x) (4) determine if f and g intersect.

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{function}\:{f}\left({x}\right)\:=\:\frac{{x}\:+\:\mathrm{3}}{{x}−\mathrm{2}}\:\mathrm{and}\:\mathrm{g}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{xe}^{{x}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{symmetry}\:\mathrm{of}\:{f}. \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Define}\:\mathrm{the}\:\mathrm{monotony}\:\mathrm{of}\:\mathrm{g}\:\mathrm{and}\:\mathrm{if}\:\mathrm{possible}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{variation} \\ $$$$\mathrm{table}\:\mathrm{for}\:\mathrm{g}\left({x}\right). \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Sketch}\:\mathrm{the}\:\mathrm{function}\:\mathrm{g}\left({x}\right) \\ $$$$\left(\mathrm{4}\right)\:\mathrm{determine}\:\mathrm{if}\:{f}\:\mathrm{and}\:\mathrm{g}\:\mathrm{intersect}. \\ $$

Answered by abdomsup last updated on 11/Aug/20

f(x)=((x+3)/(x−2)) =((x−2+5)/(x−2)) =1+(5/(x−2)) ⇒f(x)−1 =(5/(x−2)) let w(2,1) let provethat f(4−x) =2−f(x) (f(2a−x)=2b−f(x)) f(4−x)=((4−x+3)/(4−x−2)) =((7−x)/(2−x))=((x−7)/(x−2)) 2−f(x)=2−((x+3)/(x−2)) =((2x−4−x−3)/(x−2)) =((x−7)/(x−2)) ⇒f(4−x)=2−f(x) ⇒ w(2,1) is a centre of symetry

$${f}\left({x}\right)=\frac{{x}+\mathrm{3}}{{x}−\mathrm{2}}\:=\frac{{x}−\mathrm{2}+\mathrm{5}}{{x}−\mathrm{2}}\:=\mathrm{1}+\frac{\mathrm{5}}{{x}−\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)−\mathrm{1}\:=\frac{\mathrm{5}}{{x}−\mathrm{2}}\:{let}\:{w}\left(\mathrm{2},\mathrm{1}\right) \\ $$$${let}\:{provethat}\:{f}\left(\mathrm{4}−{x}\right)\:=\mathrm{2}−{f}\left({x}\right) \\ $$$$\left({f}\left(\mathrm{2}{a}−{x}\right)=\mathrm{2}{b}−{f}\left({x}\right)\right) \\ $$$${f}\left(\mathrm{4}−{x}\right)=\frac{\mathrm{4}−{x}+\mathrm{3}}{\mathrm{4}−{x}−\mathrm{2}}\:=\frac{\mathrm{7}−{x}}{\mathrm{2}−{x}}=\frac{{x}−\mathrm{7}}{{x}−\mathrm{2}} \\ $$$$\mathrm{2}−{f}\left({x}\right)=\mathrm{2}−\frac{{x}+\mathrm{3}}{{x}−\mathrm{2}}\:=\frac{\mathrm{2}{x}−\mathrm{4}−{x}−\mathrm{3}}{{x}−\mathrm{2}} \\ $$$$=\frac{{x}−\mathrm{7}}{{x}−\mathrm{2}}\:\Rightarrow{f}\left(\mathrm{4}−{x}\right)=\mathrm{2}−{f}\left({x}\right)\:\Rightarrow \\ $$$${w}\left(\mathrm{2},\mathrm{1}\right)\:{is}\:{a}\:{centre}\:{of}\:{symetry} \\ $$$$ \\ $$

Commented by Rio Michael last updated on 11/Aug/20

Thank you so much sir.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$

Answered by abdomsup last updated on 11/Aug/20

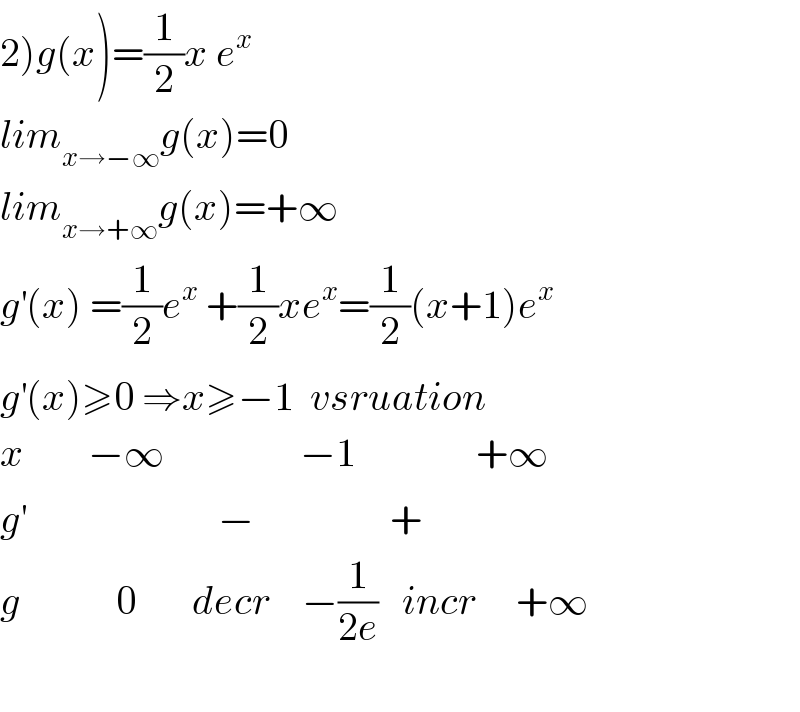
2)g(x)=(1/2)x e^x lim_(x→−∞) g(x)=0 lim_(x→+∞) g(x)=+∞ g^′ (x) =(1/2)e^x +(1/2)xe^x =(1/2)(x+1)e^x g^′ (x)≥0 ⇒x≥−1 vsruation x −∞ −1 +∞ g^′ − + g 0 decr −(1/(2e)) incr +∞

$$\left.\mathrm{2}\right){g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{x}\:{e}^{{x}} \\ $$$${lim}_{{x}\rightarrow−\infty} {g}\left({x}\right)=\mathrm{0} \\ $$$${lim}_{{x}\rightarrow+\infty} {g}\left({x}\right)=+\infty \\ $$$${g}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}} \:+\frac{\mathrm{1}}{\mathrm{2}}{xe}^{{x}} =\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{1}\right){e}^{{x}} \\ $$$${g}^{'} \left({x}\right)\geqslant\mathrm{0}\:\Rightarrow{x}\geqslant−\mathrm{1}\:\:{vsruation} \\ $$$${x}\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${g}^{'} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$${g}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:{decr}\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}{e}}\:\:\:{incr}\:\:\:\:\:+\infty \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com