
Question Number 51250 by Tawa1 last updated on 25/Dec/18
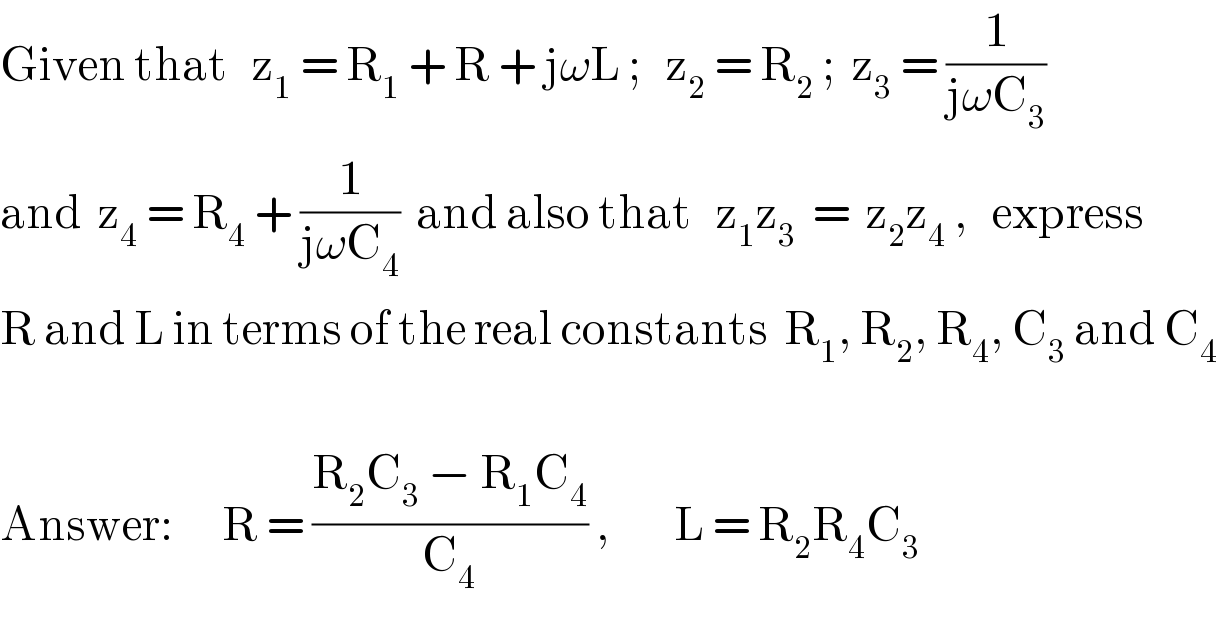
$$\mathrm{Given}\:\mathrm{that}\:\:\:\mathrm{z}_{\mathrm{1}} \:=\:\mathrm{R}_{\mathrm{1}} \:+\:\mathrm{R}\:+\:\mathrm{j}\omega\mathrm{L}\:;\:\:\:\mathrm{z}_{\mathrm{2}} \:=\:\mathrm{R}_{\mathrm{2}} \:;\:\:\mathrm{z}_{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{j}\omega\mathrm{C}_{\mathrm{3}} } \\ $$$$\mathrm{and}\:\:\mathrm{z}_{\mathrm{4}} \:=\:\mathrm{R}_{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{j}\omega\mathrm{C}_{\mathrm{4}} }\:\:\mathrm{and}\:\mathrm{also}\:\mathrm{that}\:\:\:\mathrm{z}_{\mathrm{1}} \mathrm{z}_{\mathrm{3}} \:\:=\:\:\mathrm{z}_{\mathrm{2}} \mathrm{z}_{\mathrm{4}} \:,\:\:\:\mathrm{express}\: \\ $$$$\mathrm{R}\:\mathrm{and}\:\mathrm{L}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{real}\:\mathrm{constants}\:\:\mathrm{R}_{\mathrm{1}} ,\:\mathrm{R}_{\mathrm{2}} ,\:\mathrm{R}_{\mathrm{4}} ,\:\mathrm{C}_{\mathrm{3}} \:\mathrm{and}\:\mathrm{C}_{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{Answer}:\:\:\:\:\:\:\mathrm{R}\:=\:\frac{\mathrm{R}_{\mathrm{2}} \mathrm{C}_{\mathrm{3}} \:−\:\mathrm{R}_{\mathrm{1}} \mathrm{C}_{\mathrm{4}} }{\mathrm{C}_{\mathrm{4}} }\:,\:\:\:\:\:\:\:\:\mathrm{L}\:=\:\mathrm{R}_{\mathrm{2}} \mathrm{R}_{\mathrm{4}} \mathrm{C}_{\mathrm{3}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Dec/18
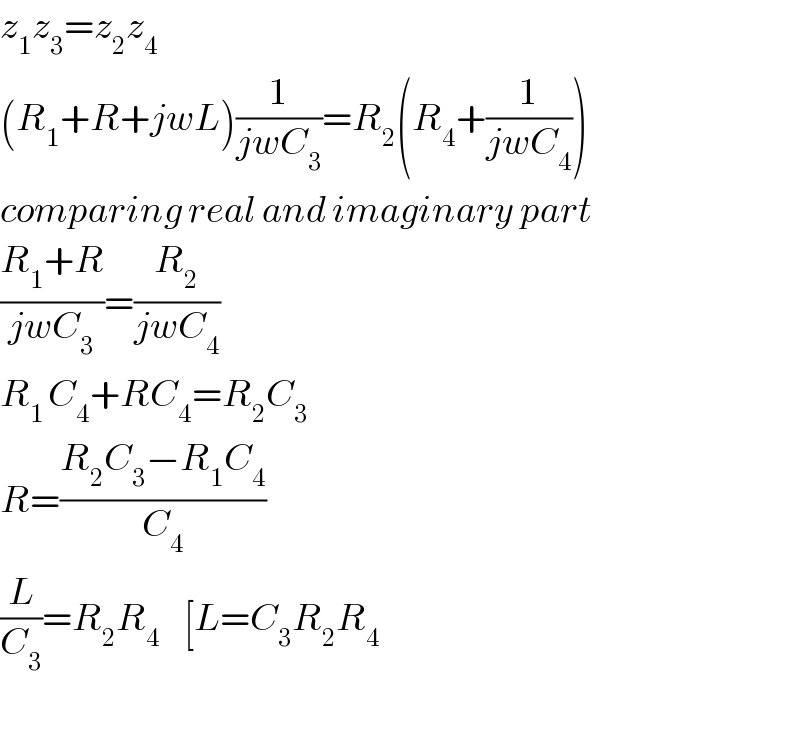
$${z}_{\mathrm{1}} {z}_{\mathrm{3}} ={z}_{\mathrm{2}} {z}_{\mathrm{4}} \\ $$$$\left({R}_{\mathrm{1}} +{R}+{jwL}\right)\frac{\mathrm{1}}{{jwC}_{\mathrm{3}} }={R}_{\mathrm{2}} \left({R}_{\mathrm{4}} +\frac{\mathrm{1}}{{jwC}_{\mathrm{4}} }\right) \\ $$$${comparing}\:{real}\:{and}\:{imaginary}\:{part} \\ $$$$\frac{{R}_{\mathrm{1}} +{R}}{{jwC}_{\mathrm{3}} }=\frac{{R}_{\mathrm{2}} }{{jwC}_{\mathrm{4}} } \\ $$$${R}_{\mathrm{1}\:} {C}_{\mathrm{4}} +{RC}_{\mathrm{4}} ={R}_{\mathrm{2}} {C}_{\mathrm{3}} \\ $$$${R}=\frac{{R}_{\mathrm{2}} {C}_{\mathrm{3}} −{R}_{\mathrm{1}} {C}_{\mathrm{4}} }{{C}_{\mathrm{4}} } \\ $$$$\frac{{L}}{{C}_{\mathrm{3}} }={R}_{\mathrm{2}} {R}_{\mathrm{4}} \:\:\:\:\left[{L}={C}_{\mathrm{3}} {R}_{\mathrm{2}} {R}_{\mathrm{4}} \right. \\ $$$$ \\ $$
Commented by Tawa1 last updated on 25/Dec/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$${thank}\:{you}... \\ $$
