
Question Number 131333 by ZiYangLee last updated on 03/Feb/21
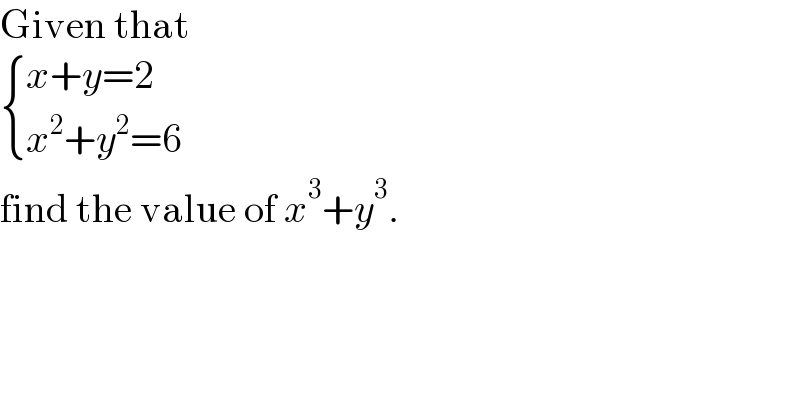
$$\mathrm{Given}\:\mathrm{that}\: \\ $$$$\begin{cases}{{x}+{y}=\mathrm{2}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{6}}\end{cases} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} . \\ $$
Answered by mr W last updated on 03/Feb/21
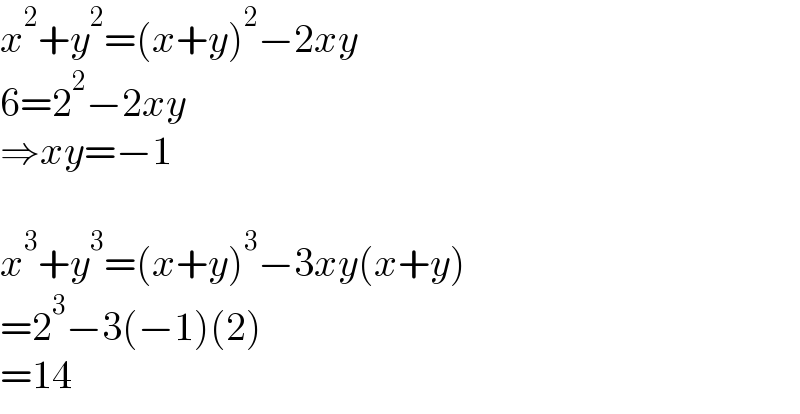
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy} \\ $$$$\mathrm{6}=\mathrm{2}^{\mathrm{2}} −\mathrm{2}{xy} \\ $$$$\Rightarrow{xy}=−\mathrm{1} \\ $$$$ \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right) \\ $$$$=\mathrm{2}^{\mathrm{3}} −\mathrm{3}\left(−\mathrm{1}\right)\left(\mathrm{2}\right) \\ $$$$=\mathrm{14} \\ $$
