
Question Number 214414 by ChantalYah last updated on 07/Dec/24
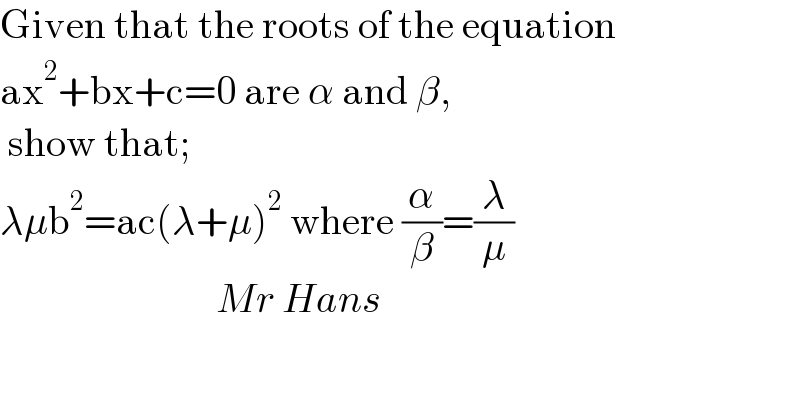
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}=\mathrm{0}\:\mathrm{are}\:\alpha\:\mathrm{and}\:\beta, \\ $$$$\:\mathrm{show}\:\mathrm{that}; \\ $$$$\lambda\mu\mathrm{b}^{\mathrm{2}} =\mathrm{ac}\left(\lambda+\mu\right)^{\mathrm{2}} \:\mathrm{where}\:\frac{\alpha}{\beta}=\frac{\lambda}{\mu} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Mr}\:{Hans} \\ $$
Answered by A5T last updated on 07/Dec/24
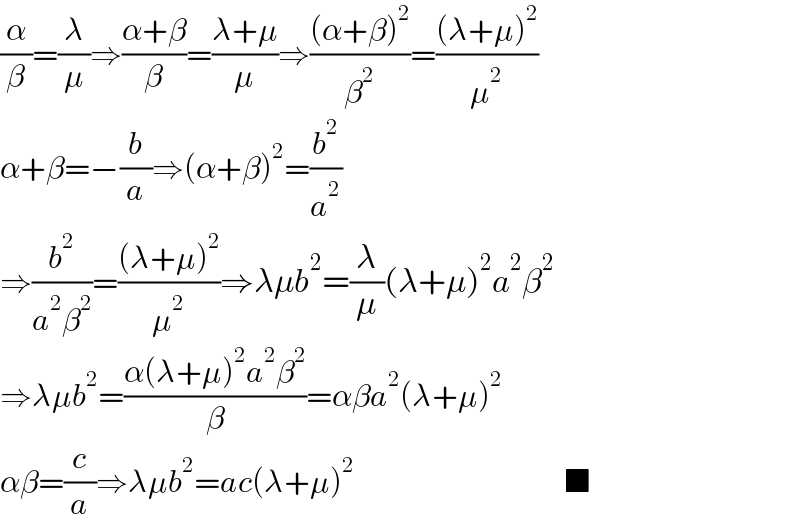
$$\frac{\alpha}{\beta}=\frac{\lambda}{\mu}\Rightarrow\frac{\alpha+\beta}{\beta}=\frac{\lambda+\mu}{\mu}\Rightarrow\frac{\left(\alpha+\beta\right)^{\mathrm{2}} }{\beta^{\mathrm{2}} }=\frac{\left(\lambda+\mu\right)^{\mathrm{2}} }{\mu^{\mathrm{2}} } \\ $$$$\alpha+\beta=−\frac{{b}}{{a}}\Rightarrow\left(\alpha+\beta\right)^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \beta^{\mathrm{2}} }=\frac{\left(\lambda+\mu\right)^{\mathrm{2}} }{\mu^{\mathrm{2}} }\Rightarrow\lambda\mu{b}^{\mathrm{2}} =\frac{\lambda}{\mu}\left(\lambda+\mu\right)^{\mathrm{2}} {a}^{\mathrm{2}} \beta^{\mathrm{2}} \\ $$$$\Rightarrow\lambda\mu{b}^{\mathrm{2}} =\frac{\alpha\left(\lambda+\mu\right)^{\mathrm{2}} {a}^{\mathrm{2}} \beta^{\mathrm{2}} }{\beta}=\alpha\beta{a}^{\mathrm{2}} \left(\lambda+\mu\right)^{\mathrm{2}} \\ $$$$\alpha\beta=\frac{{c}}{{a}}\Rightarrow\lambda\mu{b}^{\mathrm{2}} ={ac}\left(\lambda+\mu\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$
