
Question Number 24764 by NECx last updated on 25/Nov/17

$${Given}\:{that}\:{the}\:{function}\:{f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${is}\:{defined}\:{by}\:{f}\left({x}\right)={x}^{{n}} .{For}\:{what} \\ $$$${values}\:{of}\:{n},{if}\:{any},{is}\:{fof}={f}.{f}? \\ $$$${For}\:{each}\:{of}\:{these}\:{values}\:{of}\:{n}\:{find} \\ $$$${fof}. \\ $$
Answered by mrW1 last updated on 25/Nov/17
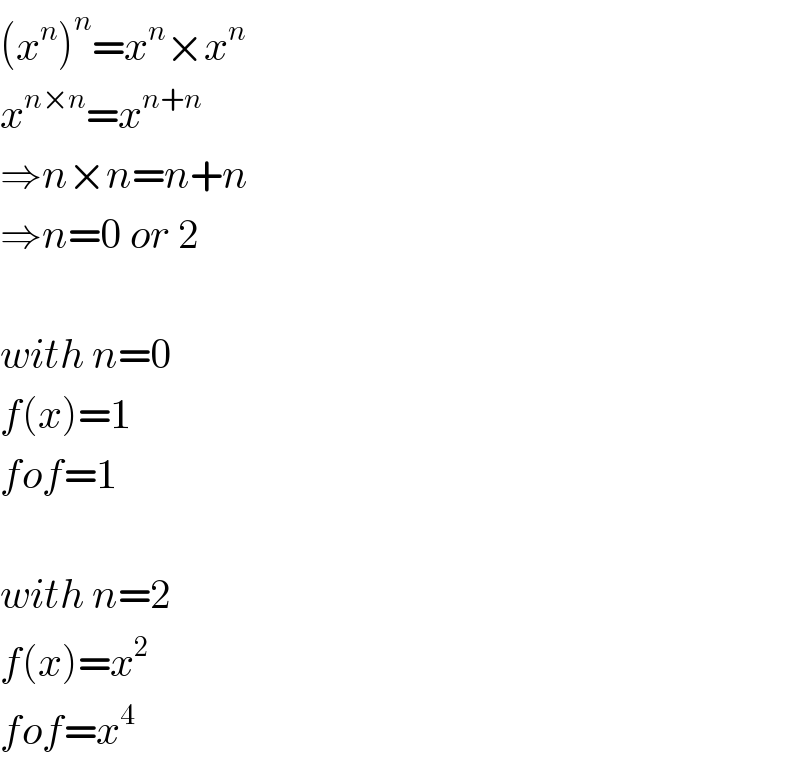
$$\left({x}^{{n}} \right)^{{n}} ={x}^{{n}} ×{x}^{{n}} \\ $$$${x}^{{n}×{n}} ={x}^{{n}+{n}} \\ $$$$\Rightarrow{n}×{n}={n}+{n} \\ $$$$\Rightarrow{n}=\mathrm{0}\:{or}\:\mathrm{2} \\ $$$$ \\ $$$${with}\:{n}=\mathrm{0} \\ $$$${f}\left({x}\right)=\mathrm{1} \\ $$$${fof}=\mathrm{1} \\ $$$$ \\ $$$${with}\:{n}=\mathrm{2} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} \\ $$$${fof}={x}^{\mathrm{4}} \\ $$
Answered by ajfour last updated on 25/Nov/17
![fof=f[f(x)]=f(x^n )=(x^n )^n =x^((n^2 )) f.f=(x^n )^2 =x^(2n) fof=f.f ⇒ n^2 =2n or n(n−2)=0 ⇒ n=0, 2 for n=0 : f(x)=x^0 =1 hence fof=1 for n=2 : f(x)=x^2 hence fof=x^4 .](Q24770.png)
$${fof}={f}\left[{f}\left({x}\right)\right]={f}\left({x}^{{n}} \right)=\left({x}^{{n}} \right)^{{n}} ={x}^{\left({n}^{\mathrm{2}} \right)} \\ $$$${f}.{f}=\left({x}^{{n}} \right)^{\mathrm{2}} ={x}^{\mathrm{2}{n}} \\ $$$${fof}={f}.{f}\:\:\Rightarrow\:\:\:\:{n}^{\mathrm{2}} =\mathrm{2}{n} \\ $$$${or}\:\:\:\:{n}\left({n}−\mathrm{2}\right)=\mathrm{0}\:\:\:\:\Rightarrow\:\:\:\boldsymbol{{n}}=\mathrm{0},\:\mathrm{2} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{n}}=\mathrm{0}\:: \\ $$$${f}\left({x}\right)={x}^{\mathrm{0}} =\mathrm{1}\:\:\:{hence}\:\:{fof}=\mathrm{1} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{n}}=\mathrm{2}\:: \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} \:\:\:{hence}\:\:\:\:{fof}={x}^{\mathrm{4}} \:. \\ $$$$ \\ $$
