
Question Number 89662 by 974342176 last updated on 18/Apr/20
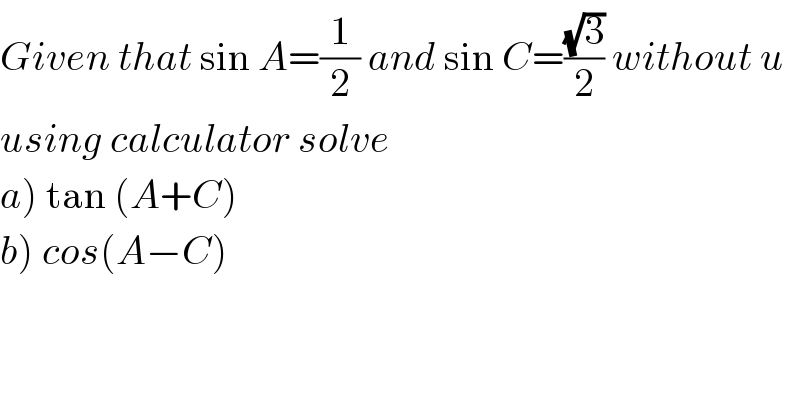
$${Given}\:{that}\:\mathrm{sin}\:{A}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:\mathrm{sin}\:{C}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{without}\:{u} \\ $$$${using}\:{calculator}\:{solve} \\ $$$$\left.{a}\right)\:\mathrm{tan}\:\left({A}+{C}\right) \\ $$$$\left.{b}\right)\:{cos}\left({A}−{C}\right) \\ $$
Answered by TANMAY PANACEA. last updated on 18/Apr/20
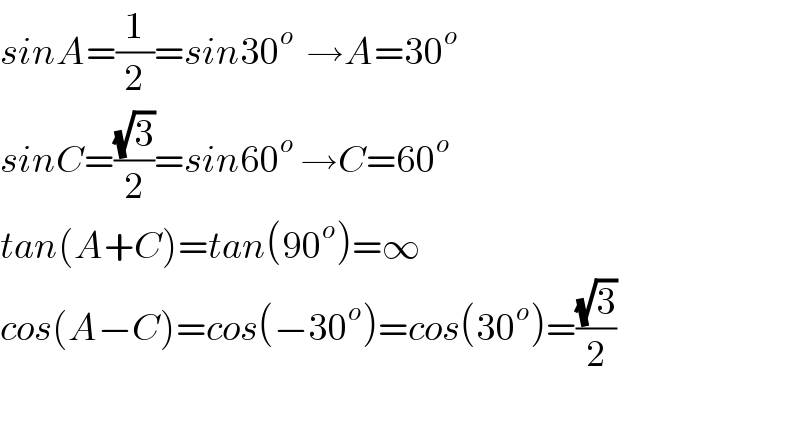
$${sinA}=\frac{\mathrm{1}}{\mathrm{2}}={sin}\mathrm{30}^{{o}} \:\:\rightarrow{A}=\mathrm{30}^{{o}} \\ $$$${sinC}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={sin}\mathrm{60}^{{o}} \:\rightarrow{C}=\mathrm{60}^{{o}} \\ $$$${tan}\left({A}+{C}\right)={tan}\left(\mathrm{90}^{{o}} \right)=\infty \\ $$$${cos}\left({A}−{C}\right)={cos}\left(−\mathrm{30}^{{o}} \right)={cos}\left(\mathrm{30}^{{o}} \right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by jagoll last updated on 19/Apr/20
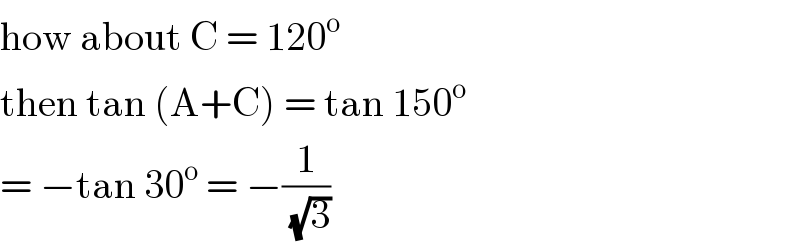
$$\mathrm{how}\:\mathrm{about}\:\mathrm{C}\:=\:\mathrm{120}^{\mathrm{o}} \: \\ $$$$\mathrm{then}\:\mathrm{tan}\:\left(\mathrm{A}+\mathrm{C}\right)\:=\:\mathrm{tan}\:\mathrm{150}^{\mathrm{o}} \: \\ $$$$=\:−\mathrm{tan}\:\mathrm{30}^{\mathrm{o}} \:=\:−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$
