
Question Number 110357 by Aina Samuel Temidayo last updated on 28/Aug/20
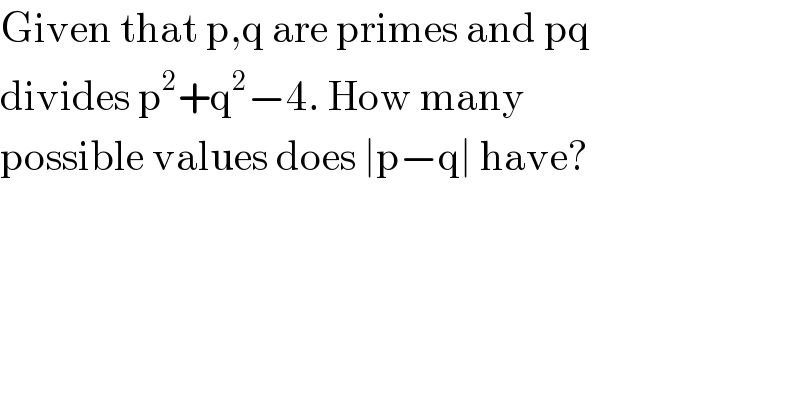
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{p},\mathrm{q}\:\mathrm{are}\:\mathrm{primes}\:\mathrm{and}\:\mathrm{pq} \\ $$$$\mathrm{divides}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{4}.\:\mathrm{How}\:\mathrm{many} \\ $$$$\mathrm{possible}\:\mathrm{values}\:\mathrm{does}\:\mid\mathrm{p}−\mathrm{q}\mid\:\mathrm{have}? \\ $$
Commented by Aina Samuel Temidayo last updated on 28/Aug/20

$$\mathrm{Any}\:\mathrm{help}\:\mathrm{please}? \\ $$
Answered by Rasheed.Sindhi last updated on 28/Aug/20
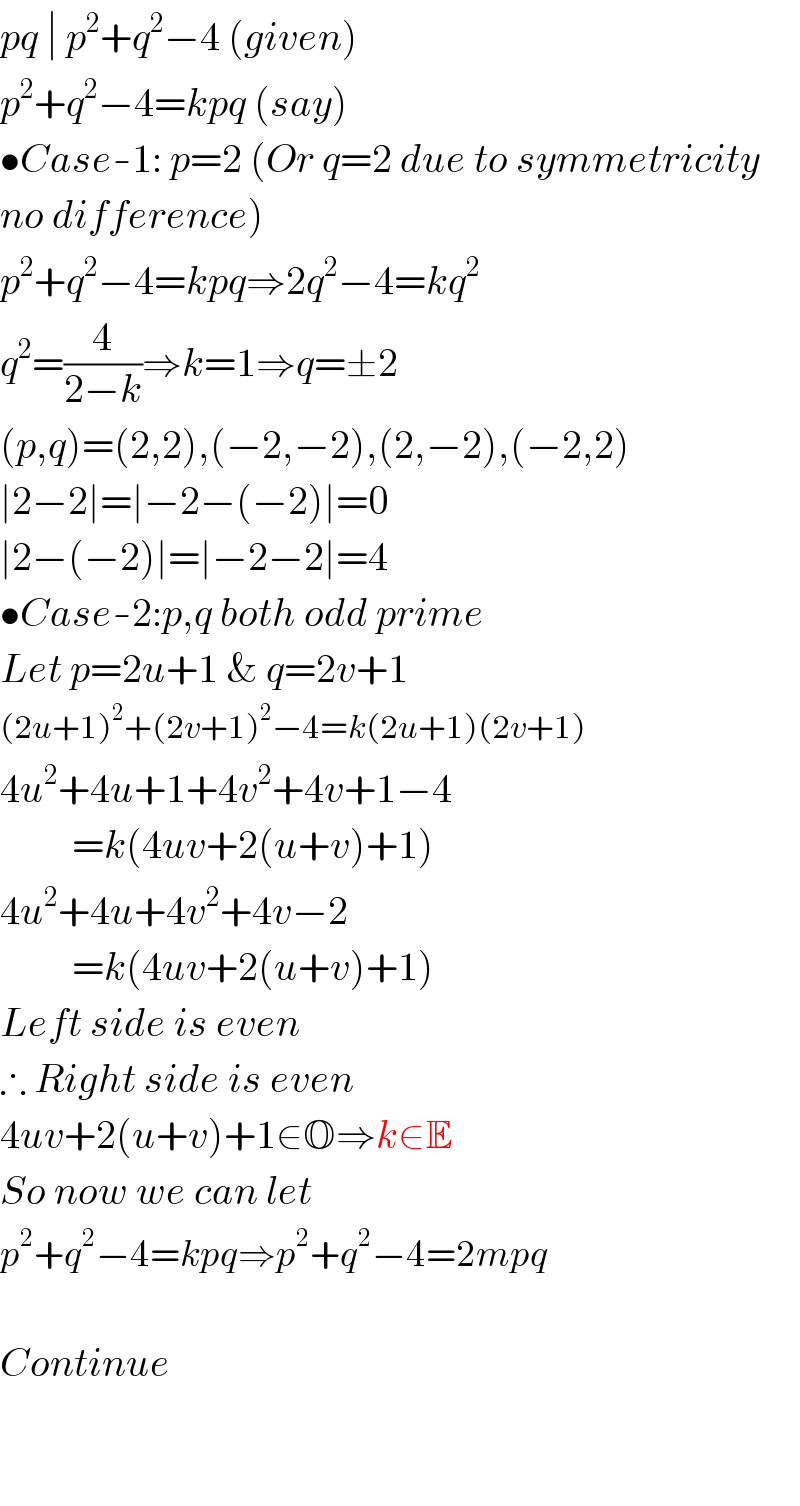
$${pq}\:\mid\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{4}\:\left({given}\right) \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{4}={kpq}\:\left({say}\right)\: \\ $$$$\bullet{Case}-\mathrm{1}:\:{p}=\mathrm{2}\:\left({Or}\:{q}=\mathrm{2}\:{due}\:{to}\:{symmetricity}\right. \\ $$$$\left.{no}\:{difference}\right) \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{4}={kpq}\Rightarrow\mathrm{2}{q}^{\mathrm{2}} −\mathrm{4}={kq}^{\mathrm{2}} \: \\ $$$${q}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{2}−{k}}\Rightarrow{k}=\mathrm{1}\Rightarrow{q}=\pm\mathrm{2} \\ $$$$\left({p},{q}\right)=\left(\mathrm{2},\mathrm{2}\right),\left(−\mathrm{2},−\mathrm{2}\right),\left(\mathrm{2},−\mathrm{2}\right),\left(−\mathrm{2},\mathrm{2}\right) \\ $$$$\mid\mathrm{2}−\mathrm{2}\mid=\mid−\mathrm{2}−\left(−\mathrm{2}\right)\mid=\mathrm{0} \\ $$$$\mid\mathrm{2}−\left(−\mathrm{2}\right)\mid=\mid−\mathrm{2}−\mathrm{2}\mid=\mathrm{4} \\ $$$$\bullet{Case}-\mathrm{2}:{p},{q}\:{both}\:{odd}\:{prime} \\ $$$${Let}\:{p}=\mathrm{2}{u}+\mathrm{1}\:\&\:{q}=\mathrm{2}{v}+\mathrm{1} \\ $$$$\left(\mathrm{2}{u}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{v}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}={k}\left(\mathrm{2}{u}+\mathrm{1}\right)\left(\mathrm{2}{v}+\mathrm{1}\right) \\ $$$$\mathrm{4}{u}^{\mathrm{2}} +\mathrm{4}{u}+\mathrm{1}+\mathrm{4}{v}^{\mathrm{2}} +\mathrm{4}{v}+\mathrm{1}−\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:={k}\left(\mathrm{4}{uv}+\mathrm{2}\left({u}+{v}\right)+\mathrm{1}\right) \\ $$$$\mathrm{4}{u}^{\mathrm{2}} +\mathrm{4}{u}+\mathrm{4}{v}^{\mathrm{2}} +\mathrm{4}{v}−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:={k}\left(\mathrm{4}{uv}+\mathrm{2}\left({u}+{v}\right)+\mathrm{1}\right) \\ $$$${Left}\:{side}\:{is}\:{even} \\ $$$$\therefore\:{Right}\:{side}\:{is}\:{even} \\ $$$$\mathrm{4}{uv}+\mathrm{2}\left({u}+{v}\right)+\mathrm{1}\in\mathbb{O}\Rightarrow{k}\in\mathbb{E} \\ $$$${So}\:{now}\:{we}\:{can}\:{let} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{4}={kpq}\Rightarrow{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{4}=\mathrm{2}{mpq} \\ $$$$ \\ $$$${Continue} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/20

$${I}'{m}\:{trying}...\mathcal{T}{he}\:{forum}\:{is}\:{full}\:{of} \\ $$$${experts},\:{so}\:{no}\:{worry}! \\ $$
Commented by Aina Samuel Temidayo last updated on 28/Aug/20

$$\mathrm{Thanks},\:\mathrm{but}\:\mathrm{Sir}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to} \\ $$$$\mathrm{finish}\:\mathrm{it}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{be}\:\mathrm{glad}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{for} \\ $$$$\mathrm{me}. \\ $$
Answered by 1549442205PVT last updated on 29/Aug/20
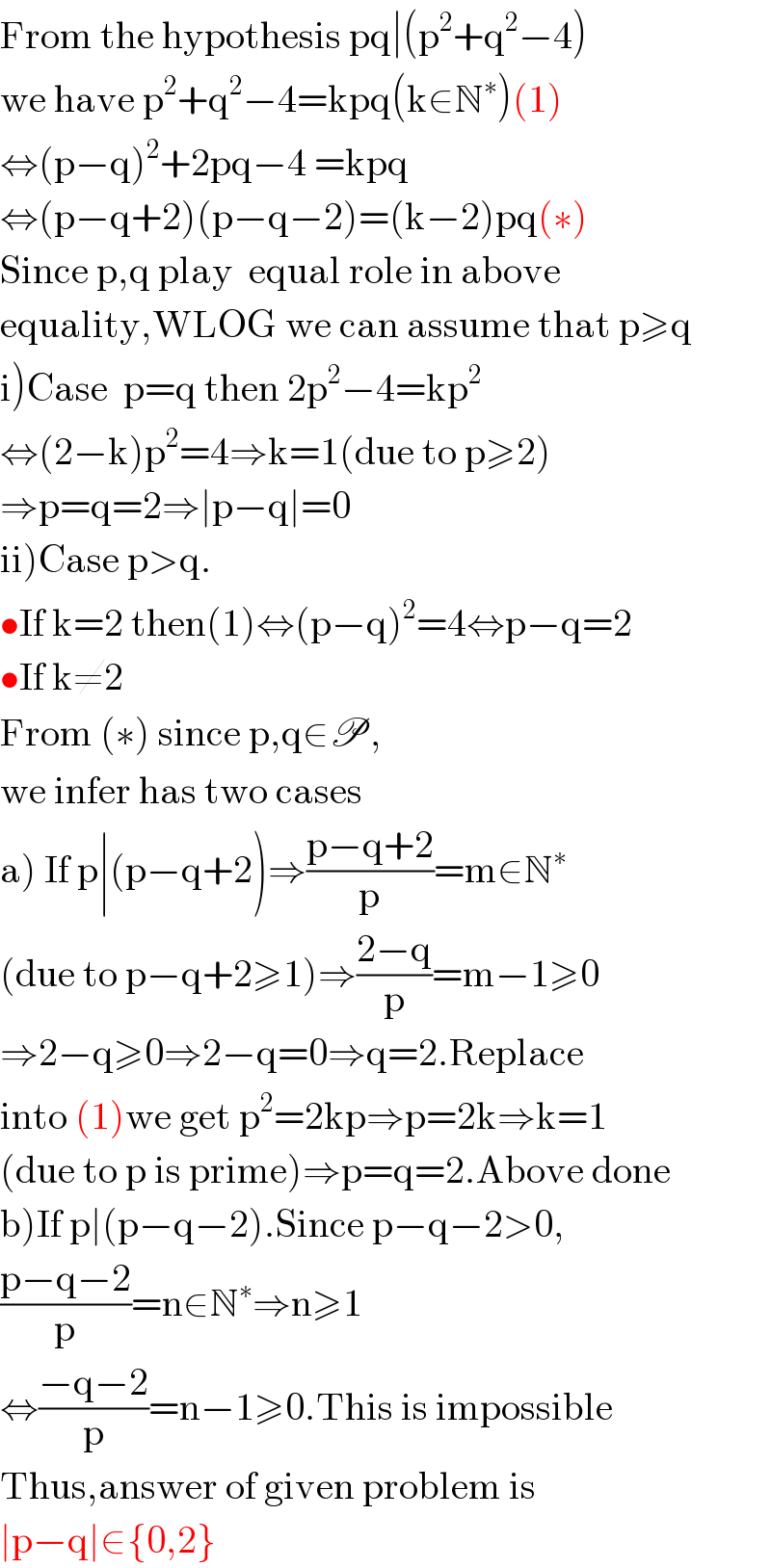
$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{pq}\mid\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{4}=\mathrm{kpq}\left(\mathrm{k}\in\mathbb{N}^{\ast} \right)\left(\mathrm{1}\right) \\ $$$$\Leftrightarrow\left(\mathrm{p}−\mathrm{q}\right)^{\mathrm{2}} +\mathrm{2pq}−\mathrm{4}\:=\mathrm{kpq} \\ $$$$\Leftrightarrow\left(\mathrm{p}−\mathrm{q}+\mathrm{2}\right)\left(\mathrm{p}−\mathrm{q}−\mathrm{2}\right)=\left(\mathrm{k}−\mathrm{2}\right)\mathrm{pq}\left(\ast\right) \\ $$$$\mathrm{Since}\:\mathrm{p},\mathrm{q}\:\mathrm{play}\:\:\mathrm{equal}\:\mathrm{role}\:\mathrm{in}\:\mathrm{above} \\ $$$$\mathrm{equality},\mathrm{WLOG}\:\mathrm{we}\:\mathrm{can}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{p}\geqslant\mathrm{q} \\ $$$$\left.\mathrm{i}\right)\mathrm{Case}\:\:\mathrm{p}=\mathrm{q}\:\mathrm{then}\:\mathrm{2p}^{\mathrm{2}} −\mathrm{4}=\mathrm{kp}^{\mathrm{2}} \\ $$$$\Leftrightarrow\left(\mathrm{2}−\mathrm{k}\right)\mathrm{p}^{\mathrm{2}} =\mathrm{4}\Rightarrow\mathrm{k}=\mathrm{1}\left(\mathrm{due}\:\mathrm{to}\:\mathrm{p}\geqslant\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{p}=\mathrm{q}=\mathrm{2}\Rightarrow\mid\mathrm{p}−\mathrm{q}\mid=\mathrm{0} \\ $$$$\left.\mathrm{ii}\right)\mathrm{Case}\:\mathrm{p}>\mathrm{q}. \\ $$$$\bullet\mathrm{If}\:\mathrm{k}=\mathrm{2}\:\mathrm{then}\left(\mathrm{1}\right)\Leftrightarrow\left(\mathrm{p}−\mathrm{q}\right)^{\mathrm{2}} =\mathrm{4}\Leftrightarrow\mathrm{p}−\mathrm{q}=\mathrm{2} \\ $$$$\bullet\mathrm{If}\:\mathrm{k}\neq\mathrm{2} \\ $$$$\mathrm{From}\:\left(\ast\right)\:\mathrm{since}\:\mathrm{p},\mathrm{q}\in\mathscr{P}, \\ $$$$\mathrm{we}\:\mathrm{infer}\:\mathrm{has}\:\mathrm{two}\:\mathrm{cases} \\ $$$$\left.\mathrm{a}\right)\:\mathrm{If}\:\mathrm{p}\mid\left(\mathrm{p}−\mathrm{q}+\mathrm{2}\right)\Rightarrow\frac{\mathrm{p}−\mathrm{q}+\mathrm{2}}{\mathrm{p}}=\mathrm{m}\in\mathbb{N}^{\ast} \\ $$$$\left(\mathrm{due}\:\mathrm{to}\:\mathrm{p}−\mathrm{q}+\mathrm{2}\geqslant\mathrm{1}\right)\Rightarrow\frac{\mathrm{2}−\mathrm{q}}{\mathrm{p}}=\mathrm{m}−\mathrm{1}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}−\mathrm{q}\geqslant\mathrm{0}\Rightarrow\mathrm{2}−\mathrm{q}=\mathrm{0}\Rightarrow\mathrm{q}=\mathrm{2}.\mathrm{Replace} \\ $$$$\mathrm{into}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{p}^{\mathrm{2}} =\mathrm{2kp}\Rightarrow\mathrm{p}=\mathrm{2k}\Rightarrow\mathrm{k}=\mathrm{1} \\ $$$$\left(\mathrm{due}\:\mathrm{to}\:\mathrm{p}\:\mathrm{is}\:\mathrm{prime}\right)\Rightarrow\mathrm{p}=\mathrm{q}=\mathrm{2}.\mathrm{Above}\:\mathrm{done} \\ $$$$\left.\mathrm{b}\right)\mathrm{If}\:\mathrm{p}\mid\left(\mathrm{p}−\mathrm{q}−\mathrm{2}\right).\mathrm{Since}\:\mathrm{p}−\mathrm{q}−\mathrm{2}>\mathrm{0}, \\ $$$$\frac{\mathrm{p}−\mathrm{q}−\mathrm{2}}{\mathrm{p}}=\mathrm{n}\in\mathbb{N}^{\ast} \Rightarrow\mathrm{n}\geqslant\mathrm{1} \\ $$$$\Leftrightarrow\frac{−\mathrm{q}−\mathrm{2}}{\mathrm{p}}=\mathrm{n}−\mathrm{1}\geqslant\mathrm{0}.\mathrm{This}\:\mathrm{is}\:\mathrm{impossible} \\ $$$$\mathrm{Thus},\mathrm{answer}\:\mathrm{of}\:\mathrm{given}\:\mathrm{problem}\:\mathrm{is} \\ $$$$\mid\mathrm{p}−\mathrm{q}\mid\in\left\{\mathrm{0},\mathrm{2}\right\} \\ $$
Commented by Aina Samuel Temidayo last updated on 29/Aug/20
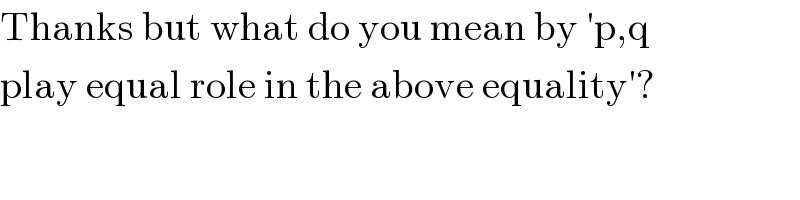
$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{by}\:'\mathrm{p},\mathrm{q}\: \\ $$$$\mathrm{play}\:\mathrm{equal}\:\mathrm{role}\:\mathrm{in}\:\mathrm{the}\:\mathrm{above}\:\mathrm{equality}'? \\ $$
Commented by 1549442205PVT last updated on 30/Aug/20

$$\mathrm{p},\mathrm{q}\:\mathrm{have}\:\:\mathrm{equal}\:\mathrm{roles}\:,\mathrm{when}\:\mathrm{change}\:\mathrm{their} \\ $$$$\mathrm{positions}\:\mathrm{for}\:\mathrm{each}\:\mathrm{other}\:\mathrm{then}\:\mathrm{the}\:\mathrm{equality} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{change} \\ $$
