
Question Number 143970 by ZiYangLee last updated on 20/Jun/21
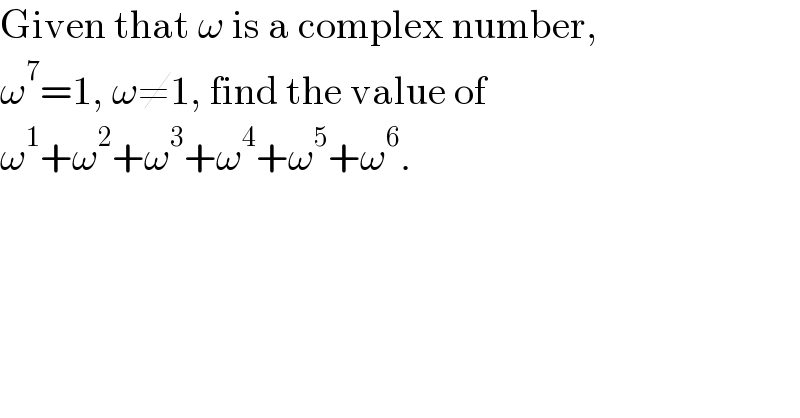
$$\mathrm{Given}\:\mathrm{that}\:\omega\:\mathrm{is}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}, \\ $$$$\omega^{\mathrm{7}} =\mathrm{1},\:\omega\neq\mathrm{1},\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\omega^{\mathrm{1}} +\omega^{\mathrm{2}} +\omega^{\mathrm{3}} +\omega^{\mathrm{4}} +\omega^{\mathrm{5}} +\omega^{\mathrm{6}} . \\ $$
Answered by Rasheed.Sindhi last updated on 20/Jun/21
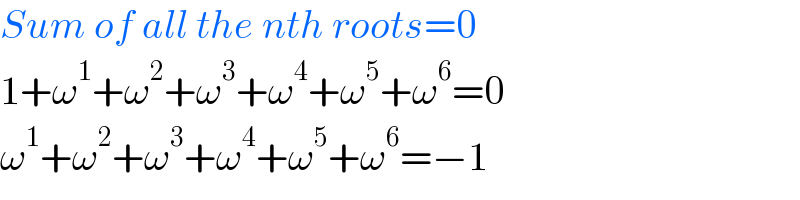
$${Sum}\:{of}\:{all}\:{the}\:{nth}\:{roots}=\mathrm{0} \\ $$$$\mathrm{1}+\omega^{\mathrm{1}} +\omega^{\mathrm{2}} +\omega^{\mathrm{3}} +\omega^{\mathrm{4}} +\omega^{\mathrm{5}} +\omega^{\mathrm{6}} =\mathrm{0} \\ $$$$\omega^{\mathrm{1}} +\omega^{\mathrm{2}} +\omega^{\mathrm{3}} +\omega^{\mathrm{4}} +\omega^{\mathrm{5}} +\omega^{\mathrm{6}} =−\mathrm{1} \\ $$
