
Question Number 65166 by Rio Michael last updated on 25/Jul/19
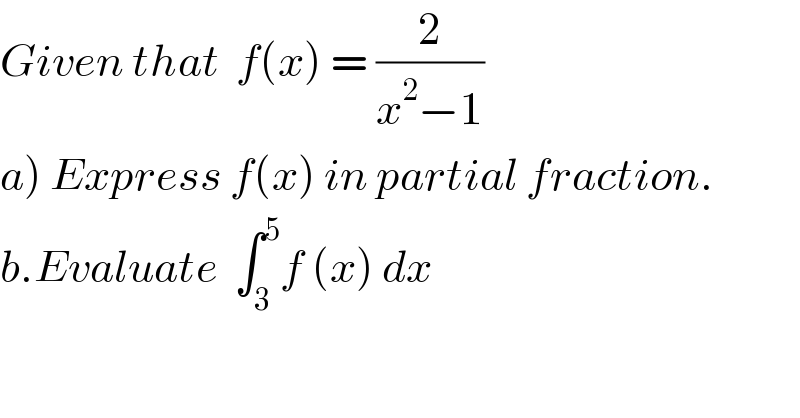
$${Given}\:{that}\:\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\left.{a}\right)\:{Express}\:{f}\left({x}\right)\:{in}\:{partial}\:{fraction}. \\ $$$${b}.{Evaluate}\:\:\int_{\mathrm{3}} ^{\mathrm{5}} {f}\:\left({x}\right)\:{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Jul/19
![a) we have f(x) =(2/((x−1)(x+1))) =(1/(x−1))−(1/(x+1)) b) ∫_3 ^5 f(x)dx =∫_3 ^5 ((1/(x−1))−(1/(x+1)))dx =[ln∣x−1∣−ln∣x+1∣]_3 ^5 =[ln∣((x−1)/(x+1))∣]_3 ^5 =ln((4/6))−ln((2/4)) =ln((2/3))−ln((1/2)) =ln(2)−ln(3)+ln2 =2ln2 −ln(3) .](Q65188.png)
$$\left.{a}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\frac{\mathrm{2}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\left.{b}\right)\:\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx}\:=\int_{\mathrm{3}} ^{\mathrm{5}} \left(\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx}\:=\left[{ln}\mid{x}−\mathrm{1}\mid−{ln}\mid{x}+\mathrm{1}\mid\right]_{\mathrm{3}} ^{\mathrm{5}} \\ $$$$=\left[{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\right]_{\mathrm{3}} ^{\mathrm{5}} \:={ln}\left(\frac{\mathrm{4}}{\mathrm{6}}\right)−{ln}\left(\frac{\mathrm{2}}{\mathrm{4}}\right)\:={ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$={ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)+{ln}\mathrm{2}\:=\mathrm{2}{ln}\mathrm{2}\:−{ln}\left(\mathrm{3}\right)\:. \\ $$
Answered by mr W last updated on 25/Jul/19
![f(x)=(2/(x^2 −1))=(1/(x−1))−(1/(x+1)) ∫_3 ^5 f(x)dx =∫_3 ^5 ((1/(x−1))−(1/(x+1)))dx =[ln ((x−1)/(x+1))]_3 ^5 =ln ((5−1)/(5+1))−ln ((3−1)/(3+1)) =ln (2/3)−ln (1/2) =ln (4/3)](Q65174.png)
$${f}\left({x}\right)=\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{3}} ^{\mathrm{5}} \left(\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$$$=\left[\mathrm{ln}\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right]_{\mathrm{3}} ^{\mathrm{5}} \\ $$$$=\mathrm{ln}\:\frac{\mathrm{5}−\mathrm{1}}{\mathrm{5}+\mathrm{1}}−\mathrm{ln}\:\frac{\mathrm{3}−\mathrm{1}}{\mathrm{3}+\mathrm{1}} \\ $$$$=\mathrm{ln}\:\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{ln}\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by Rio Michael last updated on 25/Jul/19

$${thanks} \\ $$
Commented by Rio Michael last updated on 25/Jul/19
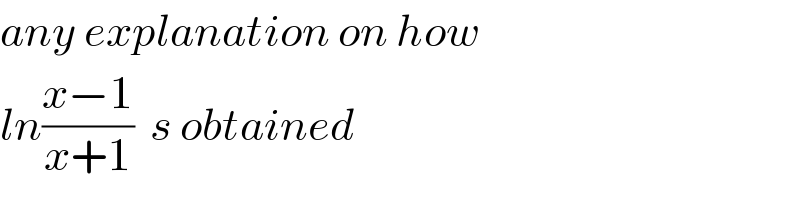
$${any}\:{explanation}\:{on}\:{how}\: \\ $$$${ln}\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\:\:{s}\:{obtained} \\ $$
Commented by MJS last updated on 25/Jul/19
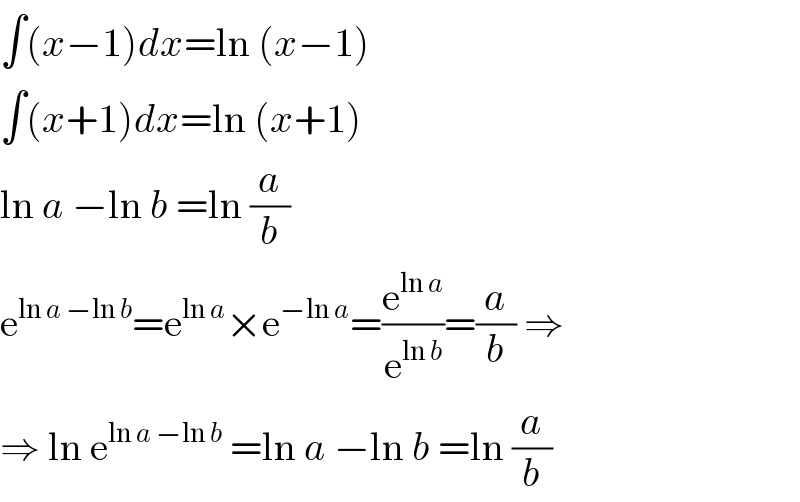
$$\int\left({x}−\mathrm{1}\right){dx}=\mathrm{ln}\:\left({x}−\mathrm{1}\right) \\ $$$$\int\left({x}+\mathrm{1}\right){dx}=\mathrm{ln}\:\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{ln}\:{a}\:−\mathrm{ln}\:{b}\:=\mathrm{ln}\:\frac{{a}}{{b}} \\ $$$$\mathrm{e}^{\mathrm{ln}\:{a}\:−\mathrm{ln}\:{b}} =\mathrm{e}^{\mathrm{ln}\:{a}} ×\mathrm{e}^{−\mathrm{ln}\:{a}} =\frac{\mathrm{e}^{\mathrm{ln}\:{a}} }{\mathrm{e}^{\mathrm{ln}\:{b}} }=\frac{{a}}{{b}}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{ln}\:\mathrm{e}^{\mathrm{ln}\:{a}\:−\mathrm{ln}\:{b}} \:=\mathrm{ln}\:{a}\:−\mathrm{ln}\:{b}\:=\mathrm{ln}\:\frac{{a}}{{b}} \\ $$
Commented by mr W last updated on 25/Jul/19
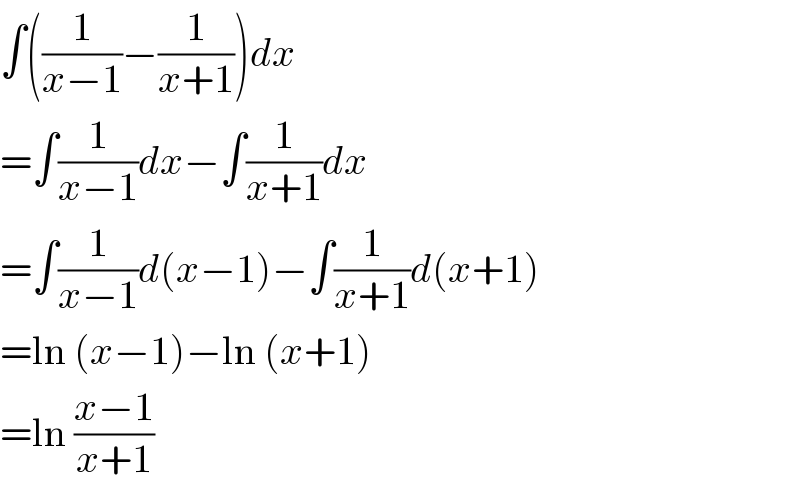
$$\int\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}−\mathrm{1}}{dx}−\int\frac{\mathrm{1}}{{x}+\mathrm{1}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}−\mathrm{1}}{d}\left({x}−\mathrm{1}\right)−\int\frac{\mathrm{1}}{{x}+\mathrm{1}}{d}\left({x}+\mathrm{1}\right) \\ $$$$=\mathrm{ln}\:\left({x}−\mathrm{1}\right)−\mathrm{ln}\:\left({x}+\mathrm{1}\right) \\ $$$$=\mathrm{ln}\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}} \\ $$
Commented by Rio Michael last updated on 25/Jul/19
$${thanks}\:{you}\:{guys}\:{so}\:{much} \\ $$
Answered by meme last updated on 25/Jul/19
![a) f(x)=(2/((x−1)(x+1)))=(1/((x−1)))−(1/((x+1))) b)∫_3 ^5 f(x) dx=∫_3 ^5 (1/((x−1))) dx −∫_3 ^5 (1/((x+1))) dx =[ln(x−1)]_3 ^5 −[ln(x+1)]_3 ^5 =ln4−ln2−ln6+ln4 =4ln2−ln2−ln6 =3ln2−ln6 =ln(4/3)](Q65187.png)
$$\left.{a}\right)\:{f}\left({x}\right)=\frac{\mathrm{2}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)} \\ $$$$\left.\:\:\:\:{b}\right)\int_{\mathrm{3}} ^{\mathrm{5}} \:\:{f}\left({x}\right)\:{dx}=\int_{\mathrm{3}} ^{\mathrm{5}} \:\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}\:{dx}\:−\int_{\mathrm{3}} ^{\mathrm{5}} \:\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)}\:{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\left[{ln}\left({x}−\mathrm{1}\right)\right]_{\mathrm{3}} ^{\mathrm{5}} −\left[{ln}\left({x}+\mathrm{1}\right)\right]_{\mathrm{3}} ^{\mathrm{5}} \\ $$$$={ln}\mathrm{4}−{ln}\mathrm{2}−{ln}\mathrm{6}+{ln}\mathrm{4} \\ $$$$=\mathrm{4}{ln}\mathrm{2}−{ln}\mathrm{2}−{ln}\mathrm{6} \\ $$$$=\mathrm{3}{ln}\mathrm{2}−{ln}\mathrm{6} \\ $$$$={ln}\frac{\mathrm{4}}{\mathrm{3}} \\ $$
