
Question Number 97413 by Rio Michael last updated on 08/Jun/20
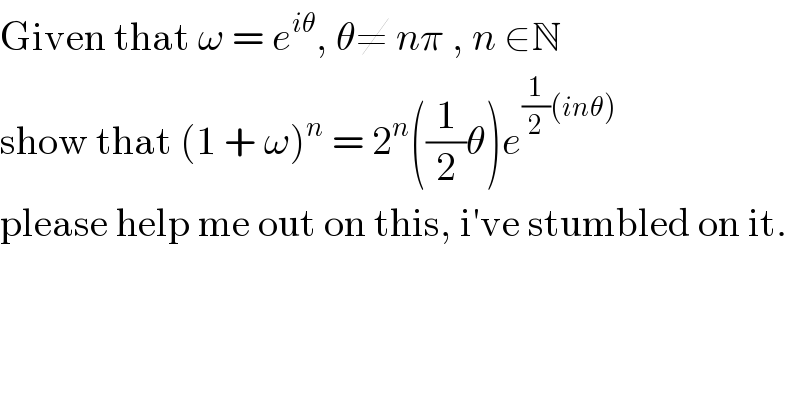
$$\mathrm{Given}\:\mathrm{that}\:\omega\:=\:{e}^{{i}\theta} ,\:\theta\neq\:{n}\pi\:,\:{n}\:\in\mathbb{N} \\ $$$$\mathrm{show}\:\mathrm{that}\:\left(\mathrm{1}\:+\:\omega\right)^{{n}} \:=\:\mathrm{2}^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\theta\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}\left({in}\theta\right)} \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{out}\:\mathrm{on}\:\mathrm{this},\:\mathrm{i}'\mathrm{ve}\:\mathrm{stumbled}\:\mathrm{on}\:\mathrm{it}. \\ $$
Answered by mathmax by abdo last updated on 08/Jun/20
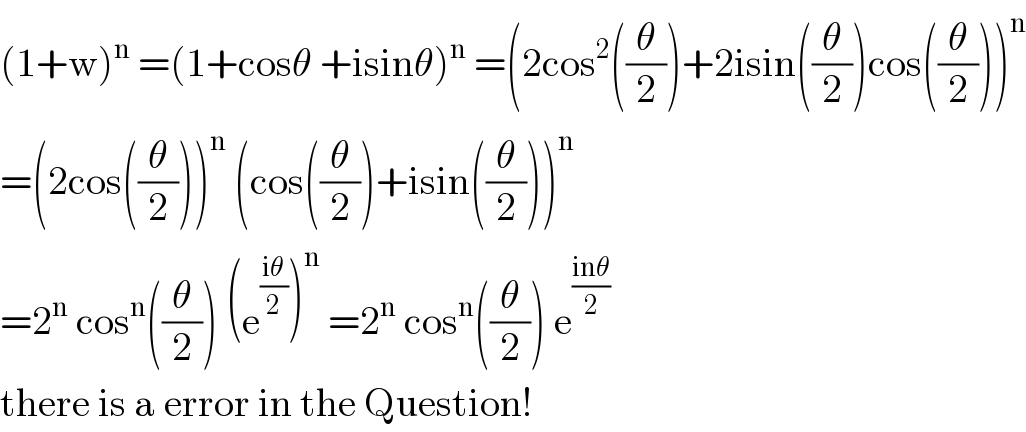
$$\left(\mathrm{1}+\mathrm{w}\right)^{\mathrm{n}} \:=\left(\mathrm{1}+\mathrm{cos}\theta\:+\mathrm{isin}\theta\right)^{\mathrm{n}} \:=\left(\mathrm{2cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{2isin}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{\mathrm{n}} \\ $$$$=\left(\mathrm{2cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{\mathrm{n}} \:\left(\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{isin}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{\mathrm{n}} \\ $$$$=\mathrm{2}^{\mathrm{n}} \:\mathrm{cos}^{\mathrm{n}} \left(\frac{\theta}{\mathrm{2}}\right)\:\left(\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{2}}} \right)^{\mathrm{n}} \:=\mathrm{2}^{\mathrm{n}} \:\mathrm{cos}^{\mathrm{n}} \left(\frac{\theta}{\mathrm{2}}\right)\:\mathrm{e}^{\frac{\mathrm{in}\theta}{\mathrm{2}}} \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{error}\:\mathrm{in}\:\mathrm{the}\:\mathrm{Question}!\: \\ $$
Commented by Rio Michael last updated on 08/Jun/20

$$\mathrm{What}\:\mathrm{a}\:\mathrm{relief}\:\mathrm{sir},\mathrm{i}\:\mathrm{tried}\:\mathrm{it}\:\mathrm{out}\:\mathrm{10}\:\mathrm{times}\:\mathrm{but}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{arrive}\:\mathrm{at}\:\mathrm{the}\:\mathrm{required}\:\mathrm{proof}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}. \\ $$
Commented by mathmax by abdo last updated on 08/Jun/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:. \\ $$
