
Question Number 210080 by Spillover last updated on 30/Jul/24
![Given that det [(a,b,c),(d,e,f),(g,h,i) ]=n find det [((d+2a),(e+2b),(f+2c)),((2a),(2b),(2c)),((4g),(4h),(4i)) ]](Q210080.png)
$${Given}\:{that}\:\:{det}\:\begin{bmatrix}{{a}}&{{b}}&{{c}}\\{{d}}&{{e}}&{{f}}\\{{g}}&{{h}}&{{i}}\end{bmatrix}={n} \\ $$$$ \\ $$$${find}\:{det}\begin{bmatrix}{{d}+\mathrm{2}{a}}&{{e}+\mathrm{2}{b}}&{{f}+\mathrm{2}{c}}\\{\mathrm{2}{a}}&{\mathrm{2}{b}}&{\mathrm{2}{c}}\\{\mathrm{4}{g}}&{\mathrm{4}{h}}&{\mathrm{4}{i}}\end{bmatrix} \\ $$$$ \\ $$
Commented by Frix last updated on 30/Jul/24
$$\mathrm{Doesn}'\mathrm{t}\:\mathrm{give}\:\mathrm{any}\:``\mathrm{nice}''\:\mathrm{result}. \\ $$
Commented by Spillover last updated on 30/Jul/24
$${what}\:{result}\:{did}\:{you}\:{get}? \\ $$
Commented by Frix last updated on 30/Jul/24
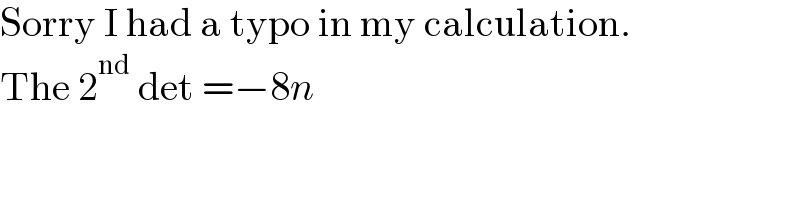
$$\mathrm{Sorry}\:\mathrm{I}\:\mathrm{had}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{my}\:\mathrm{calculation}. \\ $$$$\mathrm{The}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{det}\:=−\mathrm{8}{n} \\ $$
Commented by Spillover last updated on 30/Jul/24

$${correct} \\ $$
Answered by Spillover last updated on 30/Jul/24
![det [(a,b,c),(d,e,f),(g,h,i) ]=n det [(a,b,c),(d,e,f),((4g),(4h),(4i)) ]=4n det [((2a),(2b),(2c)),(d,e,f),((4g),(4h),(4i)) ]=8n det [((2a),(2b),(2c)),((d+2a),(e+2b),(f+2c)),((4g),(4h),(4i)) ]=8n det [((2a+d),(2b+e),(2c+f)),((2a),(2b),(2c)),((4g),(4h),(4i)) ]=−8n](Q210114.png)
$${det}\:\begin{bmatrix}{{a}}&{{b}}&{{c}}\\{{d}}&{{e}}&{{f}}\\{{g}}&{{h}}&{{i}}\end{bmatrix}={n} \\ $$$$ \\ $$$${det}\:\begin{bmatrix}{{a}}&{{b}}&{{c}}\\{{d}}&{{e}}&{{f}}\\{\mathrm{4}{g}}&{\mathrm{4}{h}}&{\mathrm{4}{i}}\end{bmatrix}=\mathrm{4}{n} \\ $$$$ \\ $$$${det}\:\begin{bmatrix}{\mathrm{2}{a}}&{\mathrm{2}{b}}&{\mathrm{2}{c}}\\{{d}}&{{e}}&{{f}}\\{\mathrm{4}{g}}&{\mathrm{4}{h}}&{\mathrm{4}{i}}\end{bmatrix}=\mathrm{8}{n} \\ $$$$ \\ $$$${det}\:\begin{bmatrix}{\mathrm{2}{a}}&{\mathrm{2}{b}}&{\mathrm{2}{c}}\\{{d}+\mathrm{2}{a}}&{{e}+\mathrm{2}{b}}&{{f}+\mathrm{2}{c}}\\{\mathrm{4}{g}}&{\mathrm{4}{h}}&{\mathrm{4}{i}}\end{bmatrix}=\mathrm{8}{n} \\ $$$$ \\ $$$${det}\:\begin{bmatrix}{\mathrm{2}{a}+{d}}&{\mathrm{2}{b}+{e}}&{\mathrm{2}{c}+{f}}\\{\mathrm{2}{a}}&{\mathrm{2}{b}}&{\mathrm{2}{c}}\\{\mathrm{4}{g}}&{\mathrm{4}{h}}&{\mathrm{4}{i}}\end{bmatrix}=−\mathrm{8}{n} \\ $$$$ \\ $$$$ \\ $$
Commented by Frix last updated on 30/Jul/24

$$\mathrm{Yes}. \\ $$
