
Question Number 35594 by Rio Mike last updated on 20/May/18

$${Given}\:{that}\:\mathrm{18},\mathrm{24},{and}\:{k}\:+\:\mathrm{14}\:{are}\: \\ $$$${three}\:{consecutive}\:{terms}\:{of}\:{an}\: \\ $$$${arithmetic}\:{progression}\:{Find} \\ $$$$\left.{a}\right)\:{the}\:{common}\:{difference} \\ $$$$\left.{b}\right)\:{the}\:{value}\:{of}\:{k} \\ $$$$\left.{c}\right){the}\:{first}\:{term}\:{if}\:{the}\:\mathrm{4}^{{th}} \:{term}\:{is} \\ $$$$\mathrm{12}. \\ $$$$\left.{d}\right)\:{the}\:{sum}\:{of}\:{the}\:{first}\:{twelve}\:{terms}\:{of} \\ $$$${the}\:{progression}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/May/18
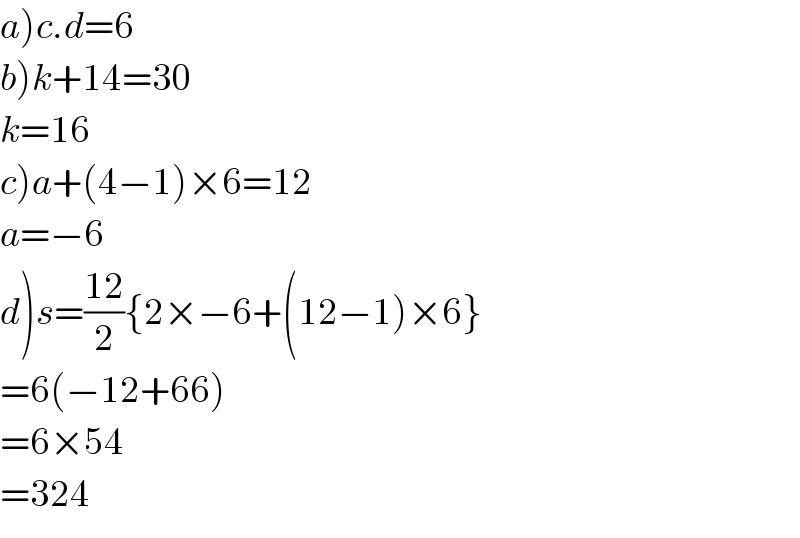
$$\left.{a}\right){c}.{d}=\mathrm{6} \\ $$$$\left.{b}\right){k}+\mathrm{14}=\mathrm{30} \\ $$$${k}=\mathrm{16} \\ $$$$\left.{c}\right){a}+\left(\mathrm{4}−\mathrm{1}\right)×\mathrm{6}=\mathrm{12} \\ $$$${a}=−\mathrm{6} \\ $$$$\left.{d}\right){s}=\frac{\mathrm{12}}{\mathrm{2}}\left\{\mathrm{2}×−\mathrm{6}+\left(\mathrm{12}−\mathrm{1}\right)×\mathrm{6}\right\} \\ $$$$=\mathrm{6}\left(−\mathrm{12}+\mathrm{66}\right) \\ $$$$=\mathrm{6}×\mathrm{54} \\ $$$$=\mathrm{324} \\ $$
