
Question Number 62109 by sandhyavs last updated on 15/Jun/19
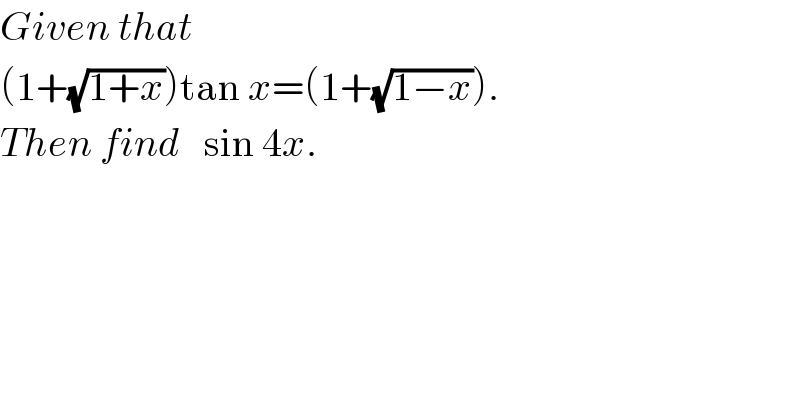
$${Given}\:{that} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}}\right)\mathrm{tan}\:{x}=\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}}\right). \\ $$$${Then}\:{find}\:\:\:\mathrm{sin}\:\mathrm{4}{x}. \\ $$
Commented by sandhyavs last updated on 15/Jun/19
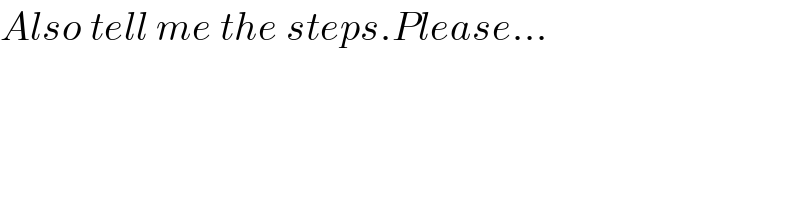
$${Also}\:{tell}\:{me}\:{the}\:{steps}.{Please}... \\ $$
Commented by sandhyavs last updated on 15/Jun/19
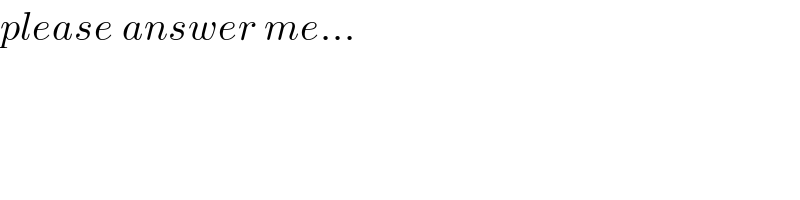
$${please}\:{answer}\:{me}... \\ $$
Answered by MJS last updated on 15/Jun/19

$$\mathrm{tan}\:{x}\:={t} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}}\right){t}\:=\mathrm{1}+\sqrt{\mathrm{1}−{x}} \\ $$$$\sqrt{\mathrm{1}−{x}}−{t}\sqrt{\mathrm{1}+{x}}={t}−\mathrm{1} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$$\mathrm{2}{t}\sqrt{\mathrm{1}−{x}}\sqrt{\mathrm{1}+{x}}=\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}+\mathrm{2}{t} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$$\left(\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} {x}+\mathrm{4}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\right){x}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\:\vee\:{x}=\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${t}=\mathrm{tan}\:{x} \\ $$$${x}=\mathrm{4sin}\:{x}\:\mathrm{cos}\:{x}\:\left(\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{sin}^{\mathrm{2}} \:{x}\right)=\mathrm{sin}\:\mathrm{4}{x} \\ $$
Commented by sandhyavs last updated on 15/Jun/19
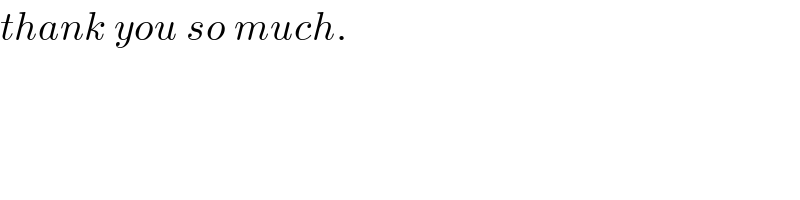
$${thank}\:{you}\:{so}\:{much}. \\ $$
