
Question Number 105861 by bemath last updated on 01/Aug/20
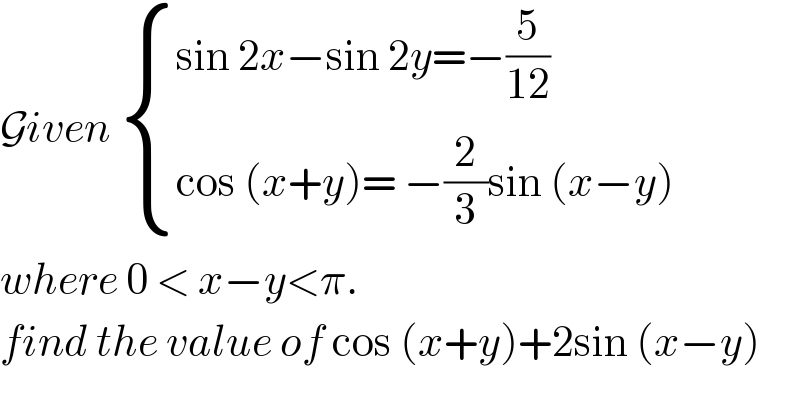
$$\mathcal{G}{iven}\:\begin{cases}{\mathrm{sin}\:\mathrm{2}{x}−\mathrm{sin}\:\mathrm{2}{y}=−\frac{\mathrm{5}}{\mathrm{12}}}\\{\mathrm{cos}\:\left({x}+{y}\right)=\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}\:\left({x}−{y}\right)}\end{cases} \\ $$$${where}\:\mathrm{0}\:<\:{x}−{y}<\pi. \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{cos}\:\left({x}+{y}\right)+\mathrm{2sin}\:\left({x}−{y}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 01/Aug/20
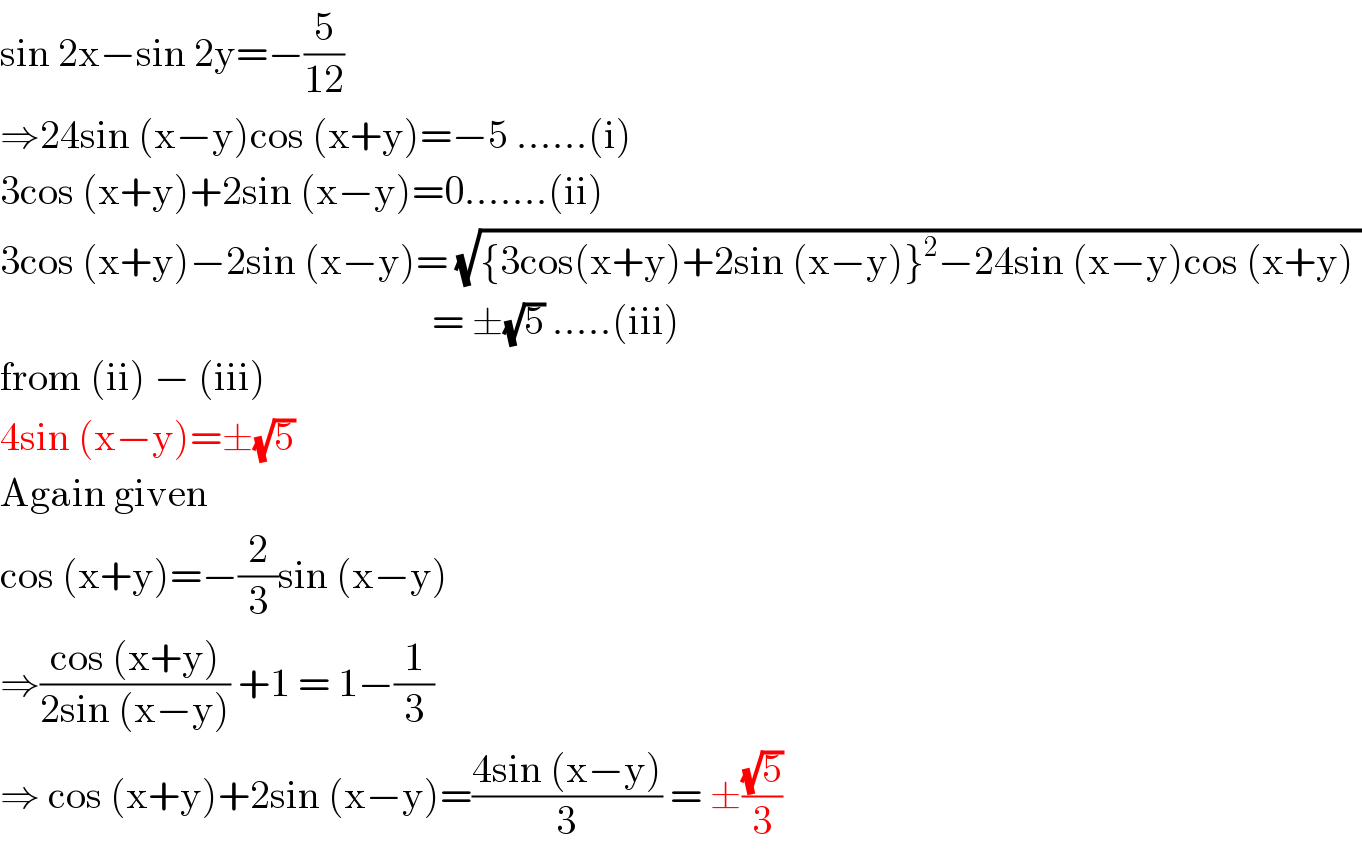
$$\mathrm{sin}\:\mathrm{2x}−\mathrm{sin}\:\mathrm{2y}=−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{24sin}\:\left(\mathrm{x}−\mathrm{y}\right)\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)=−\mathrm{5}\:......\left(\mathrm{i}\right) \\ $$$$\mathrm{3cos}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{0}.......\left(\mathrm{ii}\right) \\ $$$$\mathrm{3cos}\:\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)=\:\sqrt{\left\{\mathrm{3cos}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)\right\}^{\mathrm{2}} −\mathrm{24sin}\:\left(\mathrm{x}−\mathrm{y}\right)\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\pm\sqrt{\mathrm{5}}\:.....\left(\mathrm{iii}\right) \\ $$$$\mathrm{from}\:\left(\mathrm{ii}\right)\:−\:\left(\mathrm{iii}\right) \\ $$$$\mathrm{4sin}\:\left(\mathrm{x}−\mathrm{y}\right)=\pm\sqrt{\mathrm{5}} \\ $$$$\mathrm{Again}\:\mathrm{given} \\ $$$$\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}\:\left(\mathrm{x}−\mathrm{y}\right) \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)}{\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)}\:+\mathrm{1}\:=\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2sin}\:\left(\mathrm{x}−\mathrm{y}\right)=\frac{\mathrm{4sin}\:\left(\mathrm{x}−\mathrm{y}\right)}{\mathrm{3}}\:=\:\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 01/Aug/20
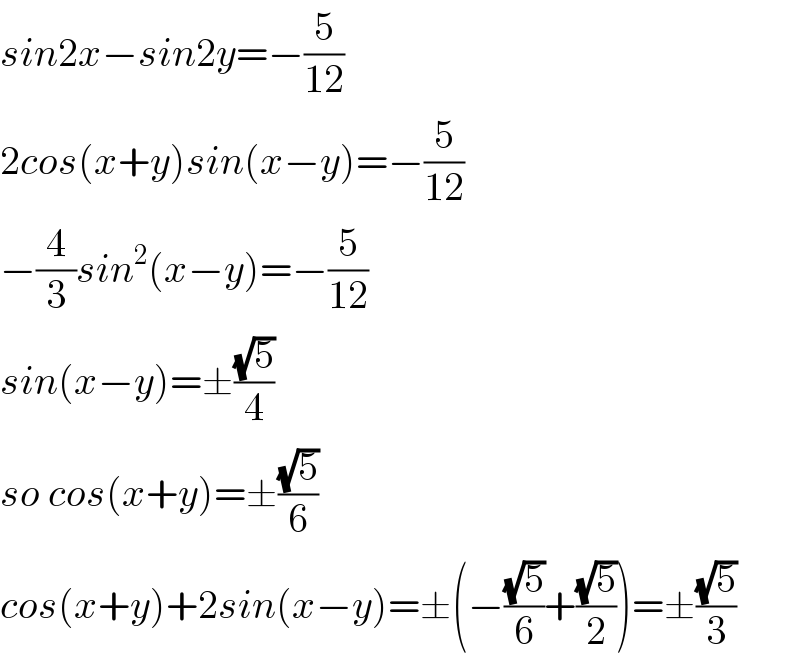
$${sin}\mathrm{2}{x}−{sin}\mathrm{2}{y}=−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\mathrm{2}{cos}\left({x}+{y}\right){sin}\left({x}−{y}\right)=−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$−\frac{\mathrm{4}}{\mathrm{3}}{sin}^{\mathrm{2}} \left({x}−{y}\right)=−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${sin}\left({x}−{y}\right)=\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${so}\:{cos}\left({x}+{y}\right)=\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{6}} \\ $$$${cos}\left({x}+{y}\right)+\mathrm{2}{sin}\left({x}−{y}\right)=\pm\left(−\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$
