
Question Number 144166 by liberty last updated on 22/Jun/21
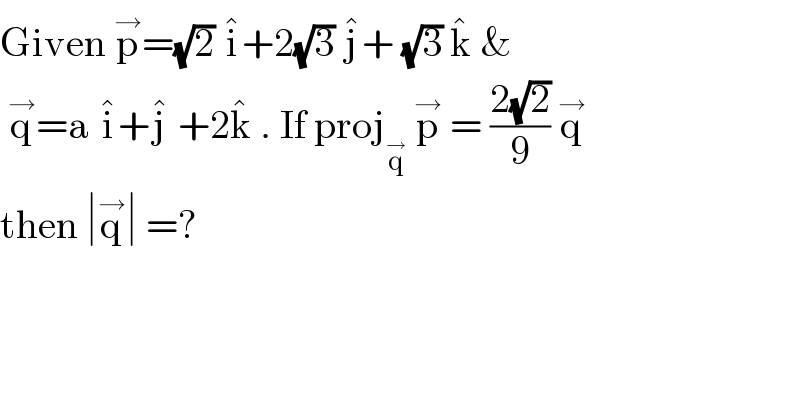
$$\mathrm{Given}\:\overset{\rightarrow} {\mathrm{p}}=\sqrt{\mathrm{2}}\:\hat {\mathrm{i}}+\mathrm{2}\sqrt{\mathrm{3}}\:\hat {\mathrm{j}}+\:\sqrt{\mathrm{3}}\:\hat {\mathrm{k}}\:\&\: \\ $$ $$\:\overset{\rightarrow} {\mathrm{q}}=\mathrm{a}\:\hat {\mathrm{i}}+\hat {\mathrm{j}}\:+\mathrm{2}\hat {\mathrm{k}}\:.\:\mathrm{If}\:\mathrm{proj}_{\overset{\rightarrow} {\mathrm{q}}} \:\overset{\rightarrow} {\mathrm{p}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9}}\:\overset{\rightarrow} {\mathrm{q}}\: \\ $$ $$\mathrm{then}\:\mid\overset{\rightarrow} {\mathrm{q}}\mid\:=?\: \\ $$
Answered by benjo_mathlover last updated on 23/Jun/21
![[ ((p^→ .q^→ )/(∣q^→ ∣^2 )) ]q^→ = ((2(√2))/9) q^→ [ ((a(√2) +2(√3)+2(√3))/(5+a^2 )) ]=((2(√2))/9) 9a(√2) +36(√3) = 10(√2) +2(√2) a^2 2(√2)a^2 −9(√2)a+10(√2)−36(√3)=0 a = ((9(√2) ± (√(162−4(40−73(√6)))))/(4(√2))) a=((9(√2) ± (√(292(√6)+2)))/(4(√2)))](Q144193.png)
$$\left[\:\frac{\overset{\rightarrow} {\mathrm{p}}.\overset{\rightarrow} {\mathrm{q}}}{\mid\overset{\rightarrow} {\mathrm{q}}\mid^{\mathrm{2}} }\:\right]\overset{\rightarrow} {\mathrm{q}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9}}\:\overset{\rightarrow} {\mathrm{q}} \\ $$ $$\left[\:\frac{\mathrm{a}\sqrt{\mathrm{2}}\:+\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{5}+\mathrm{a}^{\mathrm{2}} }\:\right]=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9}}\: \\ $$ $$\mathrm{9a}\sqrt{\mathrm{2}}\:+\mathrm{36}\sqrt{\mathrm{3}}\:=\:\mathrm{10}\sqrt{\mathrm{2}}\:+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{a}^{\mathrm{2}} \\ $$ $$\mathrm{2}\sqrt{\mathrm{2}}\mathrm{a}^{\mathrm{2}} −\mathrm{9}\sqrt{\mathrm{2}}\mathrm{a}+\mathrm{10}\sqrt{\mathrm{2}}−\mathrm{36}\sqrt{\mathrm{3}}=\mathrm{0} \\ $$ $$\mathrm{a}\:=\:\frac{\mathrm{9}\sqrt{\mathrm{2}}\:\pm\:\sqrt{\mathrm{162}−\mathrm{4}\left(\mathrm{40}−\mathrm{73}\sqrt{\mathrm{6}}\right)}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$ $$\mathrm{a}=\frac{\mathrm{9}\sqrt{\mathrm{2}}\:\pm\:\sqrt{\mathrm{292}\sqrt{\mathrm{6}}+\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
