
Question Number 120380 by bramlexs22 last updated on 31/Oct/20
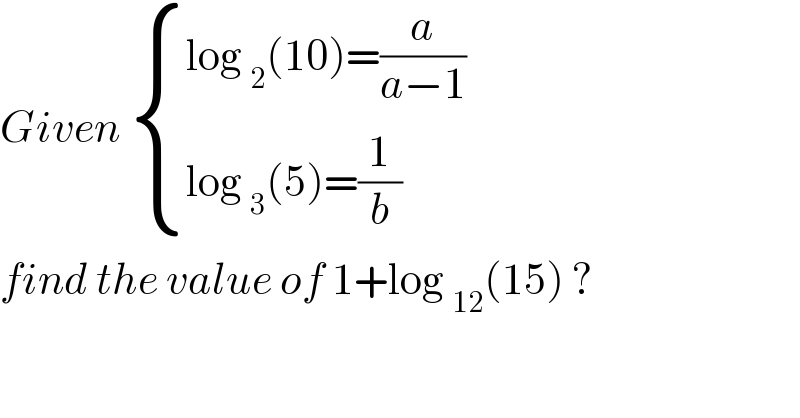
$${Given}\:\begin{cases}{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{10}\right)=\frac{{a}}{{a}−\mathrm{1}}}\\{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{5}\right)=\frac{\mathrm{1}}{{b}}}\end{cases} \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{1}+\mathrm{log}\:_{\mathrm{12}} \left(\mathrm{15}\right)\:? \\ $$
Answered by FelipeLz last updated on 31/Oct/20
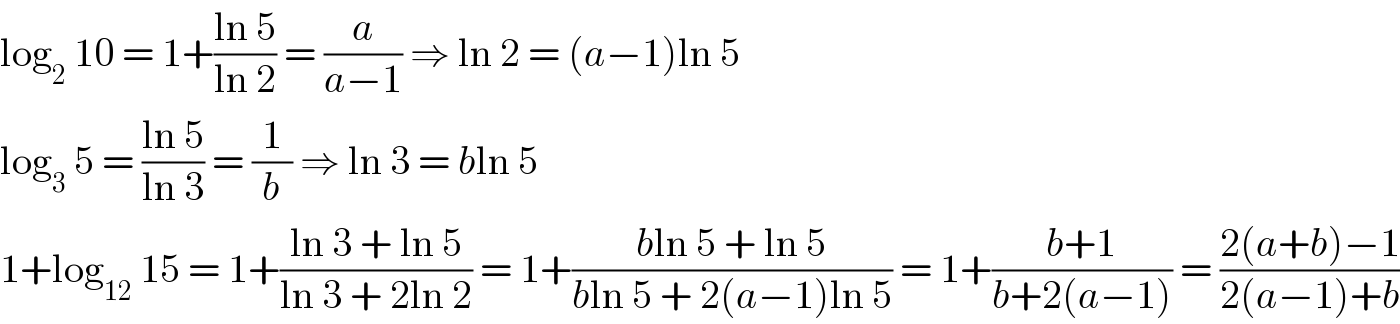
$$\mathrm{log}_{\mathrm{2}} \:\mathrm{10}\:=\:\mathrm{1}+\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{ln}\:\mathrm{2}}\:=\:\frac{{a}}{{a}−\mathrm{1}}\:\Rightarrow\:\mathrm{ln}\:\mathrm{2}\:=\:\left({a}−\mathrm{1}\right)\mathrm{ln}\:\mathrm{5} \\ $$$$\mathrm{log}_{\mathrm{3}} \:\mathrm{5}\:=\:\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{ln}\:\mathrm{3}}\:=\:\frac{\mathrm{1}}{{b}}\:\Rightarrow\:\mathrm{ln}\:\mathrm{3}\:=\:{b}\mathrm{ln}\:\mathrm{5} \\ $$$$\mathrm{1}+\mathrm{log}_{\mathrm{12}} \:\mathrm{15}\:=\:\mathrm{1}+\frac{\mathrm{ln}\:\mathrm{3}\:+\:\mathrm{ln}\:\mathrm{5}}{\mathrm{ln}\:\mathrm{3}\:+\:\mathrm{2ln}\:\mathrm{2}}\:=\:\mathrm{1}+\frac{{b}\mathrm{ln}\:\mathrm{5}\:+\:\mathrm{ln}\:\mathrm{5}}{{b}\mathrm{ln}\:\mathrm{5}\:+\:\mathrm{2}\left({a}−\mathrm{1}\right)\mathrm{ln}\:\mathrm{5}}\:=\:\mathrm{1}+\frac{{b}+\mathrm{1}}{{b}+\mathrm{2}\left({a}−\mathrm{1}\right)}\:=\:\frac{\mathrm{2}\left({a}+{b}\right)−\mathrm{1}}{\mathrm{2}\left({a}−\mathrm{1}\right)+{b}} \\ $$
Answered by john santu last updated on 31/Oct/20
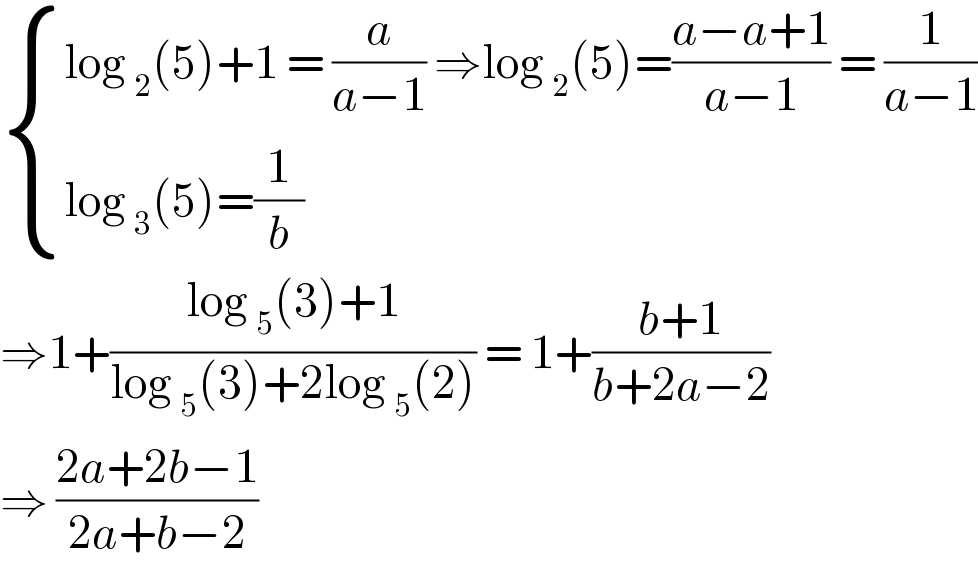
$$\begin{cases}{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{5}\right)+\mathrm{1}\:=\:\frac{{a}}{{a}−\mathrm{1}}\:\Rightarrow\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{5}\right)=\frac{{a}−{a}+\mathrm{1}}{{a}−\mathrm{1}}\:=\:\frac{\mathrm{1}}{{a}−\mathrm{1}}}\\{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{5}\right)=\frac{\mathrm{1}}{{b}}}\end{cases} \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{3}\right)+\mathrm{1}}{\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{3}\right)+\mathrm{2log}\:_{\mathrm{5}} \left(\mathrm{2}\right)}\:=\:\mathrm{1}+\frac{{b}+\mathrm{1}}{{b}+\mathrm{2}{a}−\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{2}{a}+\mathrm{2}{b}−\mathrm{1}}{\mathrm{2}{a}+{b}−\mathrm{2}} \\ $$
