
Question Number 110440 by bemath last updated on 29/Aug/20
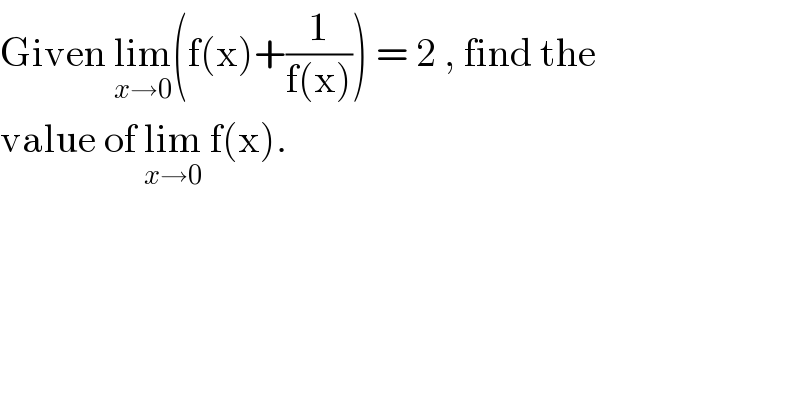
$$\mathrm{Given}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{f}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{f}\left(\mathrm{x}\right)}\right)\:=\:\mathrm{2}\:,\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{value}\:\mathrm{of}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right). \\ $$
Answered by john santu last updated on 29/Aug/20
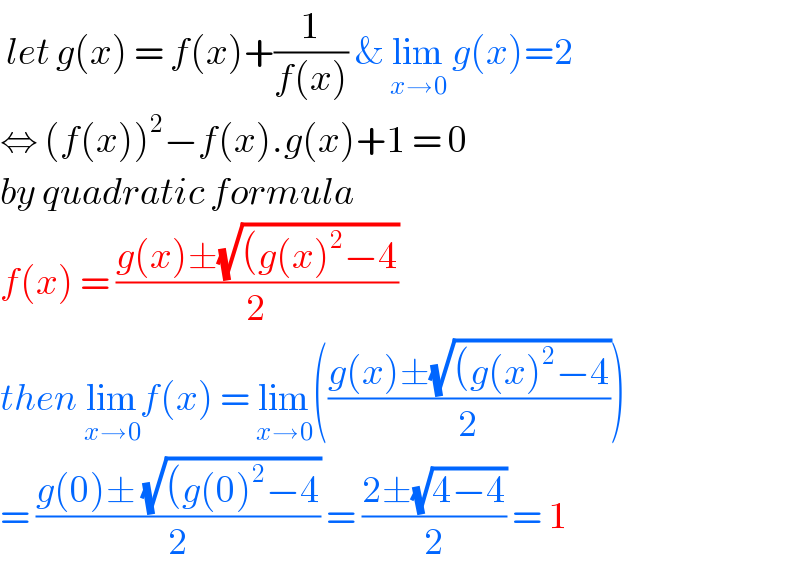
$$\:{let}\:{g}\left({x}\right)\:=\:{f}\left({x}\right)+\frac{\mathrm{1}}{{f}\left({x}\right)}\:\&\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{g}\left({x}\right)=\mathrm{2} \\ $$$$\Leftrightarrow\:\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right).{g}\left({x}\right)+\mathrm{1}\:=\:\mathrm{0} \\ $$$${by}\:{quadratic}\:{formula} \\ $$$${f}\left({x}\right)\:=\:\frac{{g}\left({x}\right)\pm\sqrt{\left({g}\left({x}\right)^{\mathrm{2}} −\mathrm{4}\right.}}{\mathrm{2}} \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{g}\left({x}\right)\pm\sqrt{\left({g}\left({x}\right)^{\mathrm{2}} −\mathrm{4}\right.}}{\mathrm{2}}\right) \\ $$$$=\:\frac{{g}\left(\mathrm{0}\right)\pm\:\sqrt{\left({g}\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{4}\right.}}{\mathrm{2}}\:=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}}}{\mathrm{2}}\:=\:\mathrm{1} \\ $$
Commented by bemath last updated on 29/Aug/20

