
Question Number 198447 by cortano12 last updated on 20/Oct/23

$$\:\:\mathrm{Given}\:\mathrm{function}\: \\ $$$$\:\:\mathrm{f}\left(\mathrm{4567},\mathrm{321567}\right)=\:\mathrm{567}+\mathrm{321}=\mathrm{888}. \\ $$$$\:\:\mathrm{f}\left(\mathrm{32156},\mathrm{12062}\right)=\:\mathrm{156}+\mathrm{120}=\mathrm{276} \\ $$$$\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\:\:\:\:\:\mathrm{f}\left(\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\:\right). \\ $$
Commented by mr W last updated on 20/Oct/23
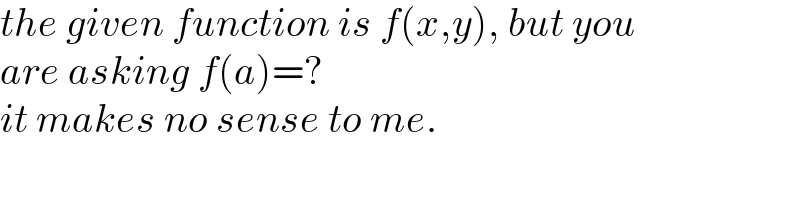
$${the}\:{given}\:{function}\:{is}\:{f}\left({x},{y}\right),\:{but}\:{you}\: \\ $$$${are}\:{asking}\:{f}\left({a}\right)=? \\ $$$${it}\:{makes}\:{no}\:{sense}\:{to}\:{me}. \\ $$
Commented by Rasheed.Sindhi last updated on 20/Oct/23

$$\boldsymbol{{sir}},\:{I}\:{think}\:{comma}\:{is}\: \\ $$$${decimal}\:{separater}\:{here}. \\ $$
Commented by cortano12 last updated on 20/Oct/23
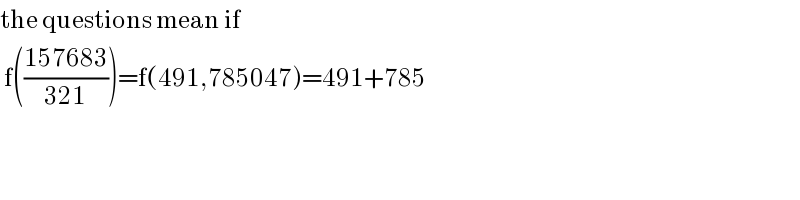
$$\mathrm{the}\:\mathrm{questions}\:\mathrm{mean}\:\mathrm{if}\: \\ $$$$\:\mathrm{f}\left(\frac{\mathrm{157683}}{\mathrm{321}}\right)=\mathrm{f}\left(\mathrm{491},\mathrm{785047}\right)=\mathrm{491}+\mathrm{785} \\ $$
Commented by mr W last updated on 20/Oct/23

$${ok}.\:``,''=``.'' \\ $$
Commented by Rasheed.Sindhi last updated on 20/Oct/23

$$\:\mathrm{f}\left(\frac{\mathrm{157683}}{\mathrm{321}}\right)=\mathrm{f}\left(\mathrm{491},\mathrm{785047}\right)=\mathrm{491}+\mathrm{785} \\ $$$$ \\ $$$${But}\:\frac{\mathrm{157683}}{\mathrm{321}}=\mathrm{491}.\mathrm{224299}\neq\mathrm{491},\mathrm{785047} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Oct/23

$$\:\:\mathrm{f}\left(\mathrm{4567},\mathrm{321567}\right)=\:\mathrm{567}+\mathrm{321}=\mathrm{888} \\ $$$$\:\:\mathrm{f}\left(\mathrm{32156},\mathrm{12062}\right)=\:\mathrm{156}+\mathrm{120}=\mathrm{276} \\ $$$$\:\:\:\:\:\mathrm{f}\left(\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\:\right)=? \\ $$$$\mathrm{f}\left(\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\:\right)=\lfloor\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\rfloor{mod}\:\mathrm{1000} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\lfloor\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}×\mathrm{1000}\rfloor{mod}\:\mathrm{1000} \\ $$$$\:\:\:\:\:\:\because\:\:\:\:\:\:\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\:=\:\frac{\mathrm{2}^{\mathrm{22}} }{\mathrm{21}}×\mathrm{10}^{\mathrm{22}} \\ $$$$=\lfloor\frac{\mathrm{2}^{\mathrm{22}} }{\mathrm{21}}×\mathrm{10}^{\mathrm{22}} \rfloor{mod}\mathrm{10}^{\mathrm{3}} +\lfloor\frac{\mathrm{2}^{\mathrm{22}} }{\mathrm{21}}×\mathrm{10}^{\mathrm{25}} \rfloor{mod}\mathrm{10}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{619}+\mathrm{47}=\mathrm{666} \\ $$$${Continue} \\ $$
Answered by MM42 last updated on 20/Oct/23
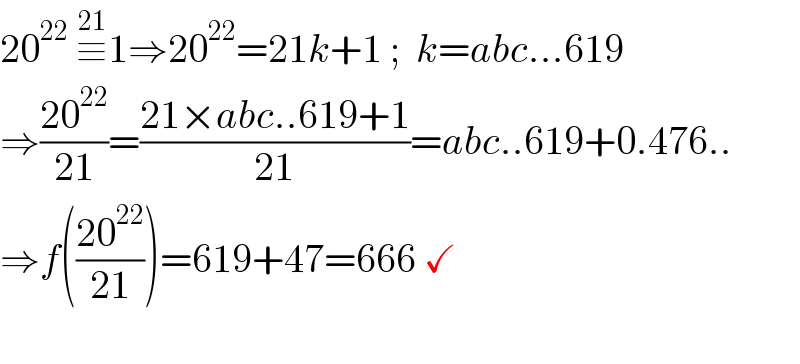
$$\mathrm{20}^{\mathrm{22}} \:\overset{\mathrm{21}} {\equiv}\mathrm{1}\Rightarrow\mathrm{20}^{\mathrm{22}} =\mathrm{21}{k}+\mathrm{1}\:;\:\:{k}={abc}...\mathrm{619} \\ $$$$\Rightarrow\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}=\frac{\mathrm{21}×{abc}..\mathrm{619}+\mathrm{1}}{\mathrm{21}}={abc}..\mathrm{619}+\mathrm{0}.\mathrm{476}.. \\ $$$$\Rightarrow{f}\left(\frac{\mathrm{20}^{\mathrm{22}} }{\mathrm{21}}\right)=\mathrm{619}+\mathrm{47}=\mathrm{666}\:\checkmark \\ $$$$ \\ $$
Commented by cortano12 last updated on 20/Oct/23

$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{k}=\mathrm{abc}...\mathrm{619}? \\ $$
Commented by MM42 last updated on 20/Oct/23
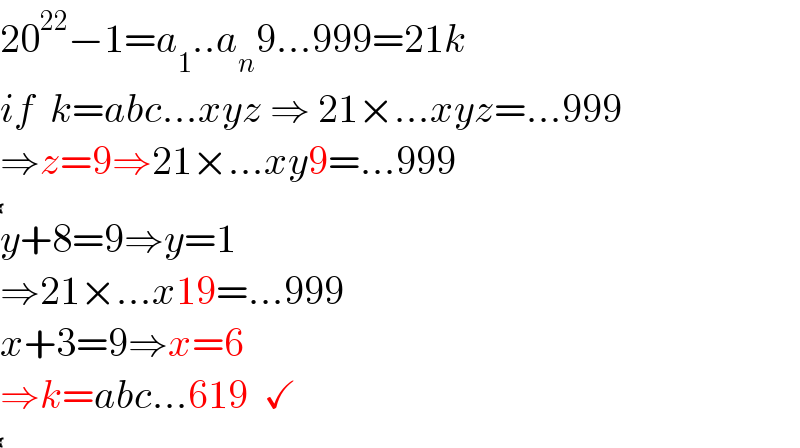
$$\mathrm{20}^{\mathrm{22}} −\mathrm{1}={a}_{\mathrm{1}} ..{a}_{{n}} \mathrm{9}...\mathrm{999}=\mathrm{21}{k} \\ $$$${if}\:\:{k}={abc}...{xyz}\:\Rightarrow\:\mathrm{21}×...{xyz}=...\mathrm{999} \\ $$$$\Rightarrow{z}=\mathrm{9}\Rightarrow\mathrm{21}×...{xy}\mathrm{9}=...\mathrm{999} \\ $$$$\underbrace{ } \\ $$$${y}+\mathrm{8}=\mathrm{9}\Rightarrow{y}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{21}×...{x}\mathrm{19}=...\mathrm{999} \\ $$$${x}+\mathrm{3}=\mathrm{9}\Rightarrow{x}=\mathrm{6} \\ $$$$\Rightarrow{k}={abc}...\mathrm{619}\:\:\checkmark\: \\ $$$$\underbrace{ } \\ $$
