
Previous in Relation and Functions Next in Relation and Functions
Question Number 188651 by cortano12 last updated on 04/Mar/23
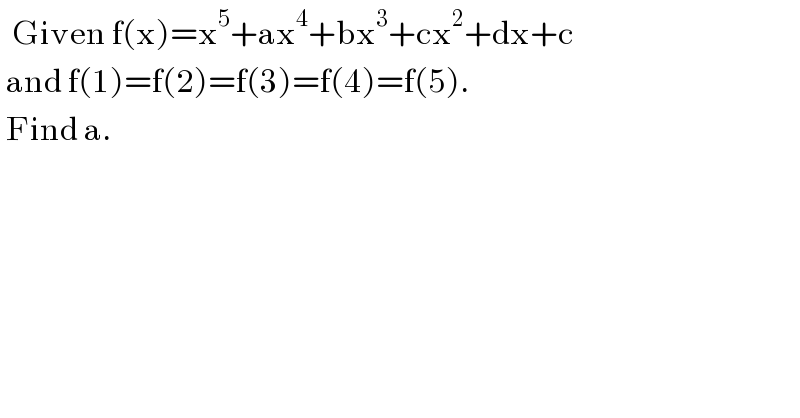
$$\:\:\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{5}} +\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{c} \\ $$$$\:\mathrm{and}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{f}\left(\mathrm{2}\right)=\mathrm{f}\left(\mathrm{3}\right)=\mathrm{f}\left(\mathrm{4}\right)=\mathrm{f}\left(\mathrm{5}\right). \\ $$$$\:\mathrm{Find}\:\mathrm{a}. \\ $$
Answered by horsebrand11 last updated on 04/Mar/23
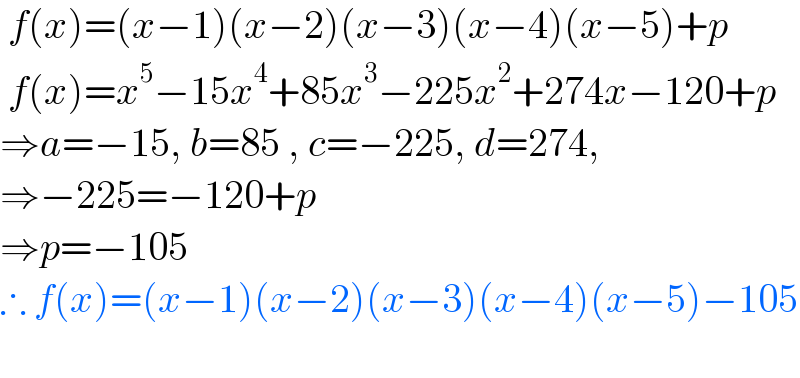
$$\:{f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)+{p} \\ $$$$\:{f}\left({x}\right)={x}^{\mathrm{5}} −\mathrm{15}{x}^{\mathrm{4}} +\mathrm{85}{x}^{\mathrm{3}} −\mathrm{225}{x}^{\mathrm{2}} +\mathrm{274}{x}−\mathrm{120}+{p} \\ $$$$\Rightarrow{a}=−\mathrm{15},\:{b}=\mathrm{85}\:,\:{c}=−\mathrm{225},\:{d}=\mathrm{274},\: \\ $$$$\Rightarrow−\mathrm{225}=−\mathrm{120}+{p} \\ $$$$\Rightarrow{p}=−\mathrm{105} \\ $$$$\therefore\:{f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)−\mathrm{105} \\ $$$$ \\ $$
