
Question Number 133610 by benjo_mathlover last updated on 23/Feb/21
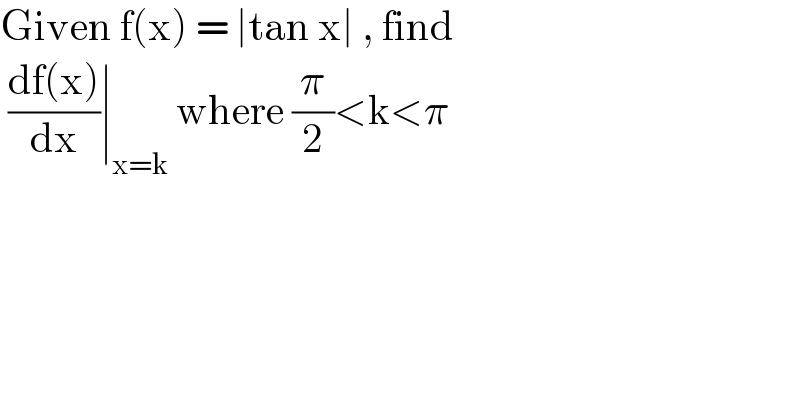
$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mid\mathrm{tan}\:\mathrm{x}\mid\:,\:\mathrm{find}\: \\ $$ $$\:\frac{\mathrm{df}\left(\mathrm{x}\right)}{\mathrm{dx}}\mid_{\mathrm{x}=\mathrm{k}} \:\mathrm{where}\:\frac{\pi}{\mathrm{2}}<\mathrm{k}<\pi \\ $$
Answered by guyyy last updated on 23/Feb/21
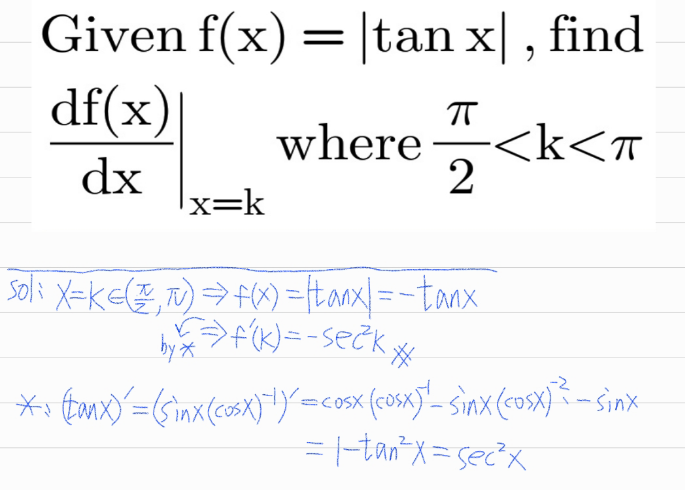
Answered by liberty last updated on 23/Feb/21
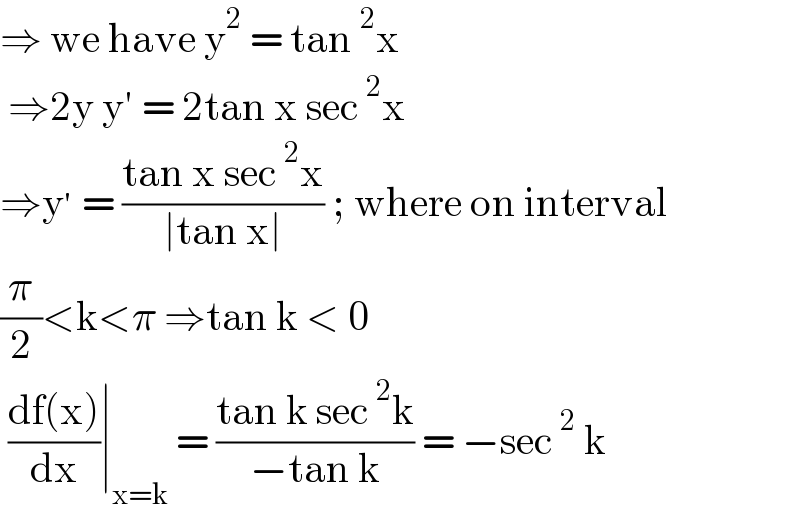
$$\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x} \\ $$ $$\:\Rightarrow\mathrm{2y}\:\mathrm{y}'\:=\:\mathrm{2tan}\:\mathrm{x}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\: \\ $$ $$\Rightarrow\mathrm{y}^{'} \:=\:\frac{\mathrm{tan}\:\mathrm{x}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mid\mathrm{tan}\:\mathrm{x}\mid}\:;\:\mathrm{where}\:\mathrm{on}\:\mathrm{interval} \\ $$ $$\frac{\pi}{\mathrm{2}}<\mathrm{k}<\pi\:\Rightarrow\mathrm{tan}\:\mathrm{k}\:<\:\mathrm{0}\: \\ $$ $$\:\frac{\mathrm{df}\left(\mathrm{x}\right)}{\mathrm{dx}}\mid_{\mathrm{x}=\mathrm{k}} \:=\:\frac{\mathrm{tan}\:\mathrm{k}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{k}}{−\mathrm{tan}\:\mathrm{k}}\:=\:−\mathrm{sec}\:^{\mathrm{2}} \:\mathrm{k}\: \\ $$
