
Question Number 125841 by bramlexs22 last updated on 14/Dec/20
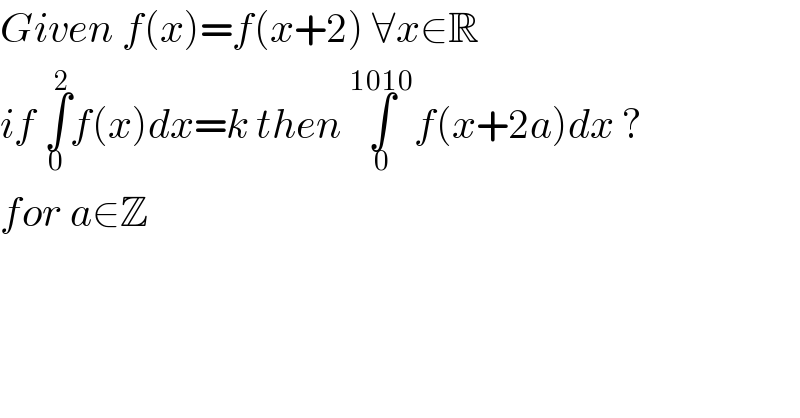
$${Given}\:{f}\left({x}\right)={f}\left({x}+\mathrm{2}\right)\:\forall{x}\in\mathbb{R} \\ $$$${if}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}={k}\:{then}\:\underset{\mathrm{0}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}+\mathrm{2}{a}\right){dx}\:? \\ $$$${for}\:{a}\in\mathbb{Z}\: \\ $$
Commented by mr W last updated on 14/Dec/20

$$\mathrm{505} \\ $$
Commented by bramlexs22 last updated on 14/Dec/20

$${step}\:{by}\:{step}\:{sir} \\ $$
Commented by bramlexs22 last updated on 14/Dec/20

$${i}\:{got}\:\mathrm{505}{k}\:{sir}.\:{not}\:\mathrm{505} \\ $$
Answered by liberty last updated on 14/Dec/20
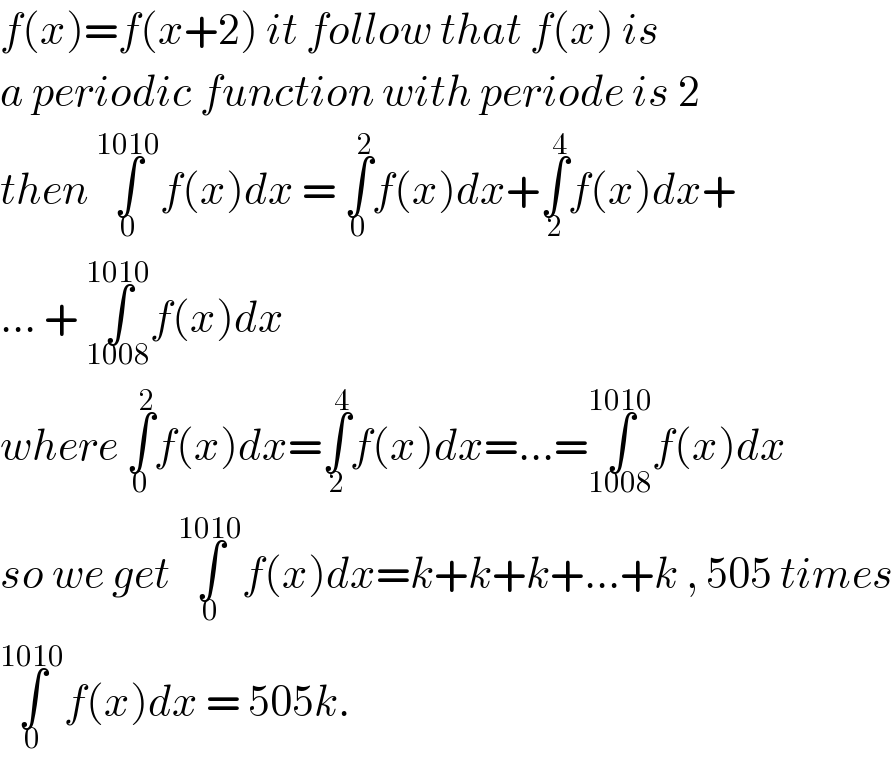
$${f}\left({x}\right)={f}\left({x}+\mathrm{2}\right)\:{it}\:{follow}\:{that}\:{f}\left({x}\right)\:{is}\: \\ $$$${a}\:{periodic}\:{function}\:{with}\:{periode}\:{is}\:\mathrm{2} \\ $$$${then}\:\underset{\mathrm{0}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}\right){dx}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}+\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right){dx}+ \\ $$$$...\:+\:\underset{\mathrm{1008}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}\right){dx} \\ $$$${where}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right){dx}=...=\underset{\mathrm{1008}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}\right){dx} \\ $$$${so}\:{we}\:{get}\:\underset{\mathrm{0}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}\right){dx}={k}+{k}+{k}+...+{k}\:,\:\mathrm{505}\:{times} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1010}} {\int}}{f}\left({x}\right){dx}\:=\:\mathrm{505}{k}. \\ $$
